【原创】已知复数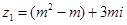 ,
,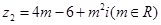 .
.
(1)若 为纯虚数,求实数
为纯虚数,求实数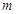 的值;
的值;
(2)当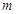 =1时,若
=1时,若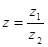 ,请问复数
,请问复数 在复平面内对应的点在第几象限?
在复平面内对应的点在第几象限?
如图四棱锥S﹣ABCD中,SD⊥AD,SD⊥CD,E是SC的中点,O是底面正方形ABCD的中心,AB=SD=6.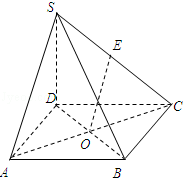
(1)求证:EO∥平面SAD;
(2)求直线EO与平面SCD所成的角.
已知椭圆C: ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2, ,离心率
,离心率 .过直线l:
.过直线l: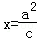 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B.
(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x0,y0)处的切线方程为:x0x+y0y=r2”.由上述结论类比得到:“过椭圆 (a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(2)利用(1)中的结论证明直线AB恒过定点( );
);
(3)当点M的纵坐标为1时,求△ABM的面积.
(本小题满分14分)函数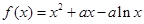
(1) 时,求函数
时,求函数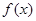 的单调区间;
的单调区间;
(2)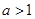 时,求函数
时,求函数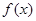 在
在 上的最大值.
上的最大值.
(本小题满分 分)已知椭圆
分)已知椭圆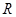 :
: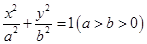 的长轴长为4,且过点
的长轴长为4,且过点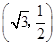 .
.
(1)求椭圆 的方程;
的方程;
(2)设 、
、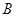 、
、 是椭圆上的三点,若
是椭圆上的三点,若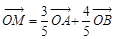 ,点
,点 为线段
为线段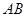 的中点,
的中点, 、
、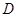 两点的坐标分别为
两点的坐标分别为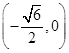 、
、 ,求证:
,求证: .
.
(本小题满分14分)
设数列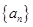 的前
的前 项和为
项和为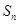 ,点
,点 在直线
在直线 上,
上,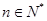 .
.
(1)证明数列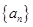 为等比数列,并求出其通项;
为等比数列,并求出其通项;
(2)设 ,记
,记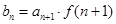 ,求数列
,求数列 的前
的前 和
和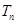 .
.