某车间生产某种产品,固定成本2万元,每生产 1件产品成本增加 100元.根据经验,当年产量少于400件时,总收益R(成本与总利润的和,单位:元)是年产量Q(单位:件)的二次函数,当年产量不少于400件时,R是Q的一次函数,以下是年产量Q与总收益R的部分数据:
| Q(件) |
50 |
200 |
350 |
500 |
650 |
| R(元) |
23750 |
80000 |
113750 |
125000 |
132500 |
试问每年生产多少件产品时,总利润最大?最大总利润是多少元?
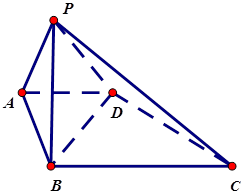
在四棱锥 中,底面
中,底面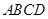 为直角梯形,
为直角梯形,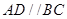 ,
,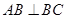 侧面
侧面 底面
底面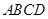 ,
,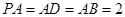 ,
, .
.
(1)若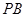 中点为
中点为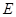 .求证:
.求证: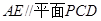 ;
;
(2)若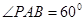 ,求直线
,求直线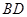 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知数列 (
( ,
, )满足
)满足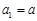 ,
, 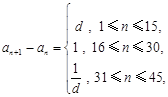 其中
其中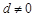 ,
, .
.
(1)当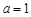 时,求
时,求 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;
(2)设集合 .若
.若 ,
,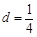 ,求证:
,求证: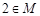 .
.
已知函数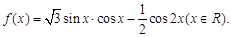
(1)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(2)设 的内角A、B、C的对边分别为a、b、c,且
的内角A、B、C的对边分别为a、b、c,且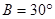 ,
, ,判断△ABC的形状,并求三角形ABC的面积.
,判断△ABC的形状,并求三角形ABC的面积.
(本小题满分14分)已知数列 (
( ,
, )满足
)满足 ,
,  其中
其中 ,
, .
.
(1)当 时,求
时,求 关于
关于 的表达式,并求
的表达式,并求 的取值范围;
的取值范围;
(2)设集合 .
.
①若 ,
, ,求证:
,求证: ;
;
②是否存在实数 ,
, ,使
,使 ,
, ,
, 都属于
都属于 ?若存在,请求出实数
?若存在,请求出实数 ,
, ;若不存在,请说明理由.
;若不存在,请说明理由.
(本小题满分15分)如图,在平面直角坐标系 中,离心率为
中,离心率为 的椭圆
的椭圆
 的左顶点为
的左顶点为 ,过原点
,过原点 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于 两点,直线
两点,直线 分别与
分别与 轴交于
轴交于 两点.若直线
两点.若直线 斜率为
斜率为 时,
时, .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)试问以 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.