用总长为14.8m的钢条制成一个长方体容器的框架,要求底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积。
(本小题满分14分) 已知函数
(Ⅰ)求它的最小正周期T;
(Ⅱ)若 ,求
,求 的值;
的值;
(Ⅲ)求 的单调增区间.
的单调增区间.
(本小题满分12分)已知x、y间的一组数据如下表:
| x |
1 |
3 |
6 |
7 |
8 |
| y |
1 |
2 |
3 |
4 |
5 |
(Ⅰ)从x、y中各取一个数,求 的概率;
的概率;
(Ⅱ)针对表中数据,甲给出拟合曲线的方程是: ,测得相关指数
,测得相关指数 ;乙给出的拟合曲线的方程是:
;乙给出的拟合曲线的方程是: ,测得相关指数
,测得相关指数 。请判断用哪一个方程拟合效果会更好,并用较好的曲线方程估计x=10时y的值。
。请判断用哪一个方程拟合效果会更好,并用较好的曲线方程估计x=10时y的值。
(本小题满分13分)
等差数列 中,首项
中,首项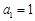 ,公差
,公差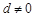 ,前n项和为
,前n项和为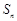 ,已知数列
,已知数列 成等比数列,其中
成等比数列,其中 ,
,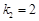 ,
, .
.
(Ⅰ)求数列 ,
,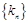 的通项公式;
的通项公式;
(Ⅱ)令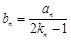 ,数列
,数列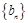 的前n项和为
的前n项和为 .若存在一个最小正整数M,使得当
.若存在一个最小正整数M,使得当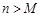 时,
时, (
( )恒成立,试求出这个最小正整数M的值.
)恒成立,试求出这个最小正整数M的值.
(本小题满分13分)
函数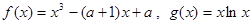 .
.
(Ⅰ)若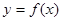 ,
,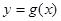 在
在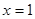 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程;
(Ⅱ)若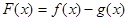 单调递增,求
单调递增,求 的范围.
的范围.
(本小题满分12分)
已知数列 的各项均为正数,且前
的各项均为正数,且前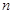 项之和
项之和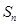 满足
满足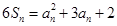 ,且
,且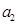 ,
,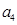 ,
,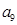 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)若数列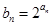 的前
的前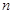 项和为
项和为 ,求
,求 .
.