(本小题满分14分)已知:在函数 的图象上,以
的图象上,以 为切点的切线的倾斜角为
为切点的切线的倾斜角为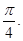
(Ⅰ)求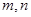 的值;
的值;
(Ⅱ)是否存在最小的正整数 ,使得不等式
,使得不等式 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 ,如果不存在,请说明理由。
,如果不存在,请说明理由。
(本小题12分) 如图,四棱锥P-ABCD的底面是正方形, PA⊥底面ABCD, PA=2,
∠PDA="45°," 点E、F分别为棱AB、PD的中点. 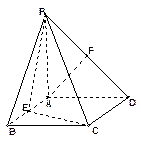
(1)求证: AF∥平面PCE;
(2)求证: 平面PCE⊥平面PCD;
(3)求AF与平面PCB所成的角的大小.
(本小题12分) 已知两条直线l1: ax-by+4=0和l2: (a-1)x+y+b="0," 求满足下列条件的a, b的值.
(1)l1⊥l2, 且l1过点(-3, -1);
(2)l1∥l2, 且坐标原点到这两条直线的距离相等.
(本小题12分) 在△ABC中, 角A、B、C所对的边分别为a、b、c, 且tanA=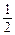 , sinB=
, sinB= .
.
(1)求tanC的值;
(2)若△ABC最长的边为1, 求b.
(本小题满分l2分)
已知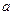 是非零实数,如果函数
是非零实数,如果函数 在区间
在区间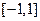 上有零点,求
上有零点,求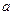 的取值范围.
的取值范围.
设函数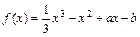 ,
,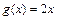 ,当
,当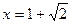 时,
时,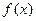 取得极值。
取得极值。
(Ⅰ)求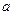 的值;
的值;
(Ⅱ)当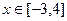 时,函数
时,函数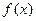 与
与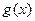 的图象有三个公共点,求
的图象有三个公共点,求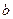 的取值范围。
的取值范围。