(本小题满分16分)已知数列 中,
中, ,前
,前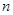 项和为
项和为
(Ⅰ)证明数列 是等差数列,并求出数列
是等差数列,并求出数列 的通项公式;
的通项公式;
(Ⅱ)设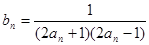 ,数列
,数列 的前
的前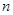 项和为
项和为 ,求使不等式
,求使不等式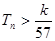 对一切
对一切 都成立的最大正整数
都成立的最大正整数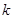 的值。
的值。
已知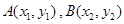 是
是 的图象上任意两点,设点
的图象上任意两点,设点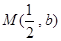 ,且
,且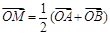 ,若
,若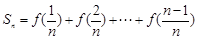 ,其中
,其中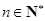 ,且
,且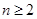 .
.
(1)求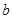 的值;
的值;
(2)求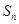 ;
;
(3)数列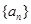 中
中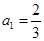 ,当
,当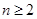 时,
时,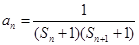 ,设数列
,设数列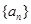 的前
的前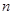 项和为
项和为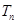 ,求
,求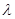 的取值范围使
的取值范围使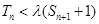 对一切
对一切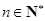 都成立.
都成立.
某企业去年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降,若不进行技术改造,预测今年起每年比上一年纯利润减少20万元.今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第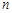 年(今年为第一年)的利润为
年(今年为第一年)的利润为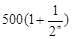 万元(
万元(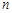 为正整数);设从今年起的前
为正整数);设从今年起的前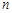 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为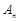 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为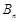 万元(需扣除技术改造资金).
万元(需扣除技术改造资金).
(1)求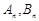 的表达式;
的表达式;
(2)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润.
(1) 为锐角,且
为锐角,且 ,求
,求 的值;
的值;
(2)已知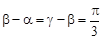 ,求
,求 的值.
的值.
已知数列 是等差数列前
是等差数列前 项和
项和 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)求数列 的前
的前 项和
项和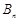 .
.
在 中,
中, 分别是角
分别是角 的对边,
的对边, ,且
,且 ∥
∥ .
.
(1)求角 的大小;(2)求
的大小;(2)求 的最小值.
的最小值.