甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束.除第五局甲队获胜的概率是 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是 .假设各局比赛结果相互独立.
.假设各局比赛结果相互独立.
(1)分别求甲队以3:0,3:1,3:2获胜的概率;
(2)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求甲队得分X的分布列及数学期望.
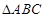 中,
中,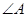 、
、 、
、 所对的边分别为
所对的边分别为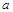 、
、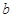 、
、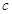
(Ⅰ) 若
若 、
、 、
、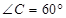 ,求
,求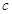 .
. (Ⅱ)若
(Ⅱ)若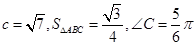 ,
,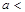
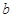 ,求
,求 、
、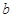 。
。
在△ABC中,a、b、c分别是角A、B、C所对的边,
且acosB十bcosA="1"
(1)求c
(2)若tan(A+B)=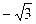 ,求
,求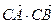 的最大值
的最大值
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=,求数列{cn}的前n项和Tn.
本题满分12分)
一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往相距400 km的灾区.为安全起见,每两辆汽车的前后间距不得小于 km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时
km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时 间,问运输时间最少需要多少小时?
间,问运输时间最少需要多少小时?
已知不等式x2-2x-3<0的解集为A,不等式x2+4x-5<0的解集为B,
(1)求A∪B;
(2)若不等式x2+ax+b<0的解集是A∪B,求ax2+x+b<0的解集