(本小题满分14分)体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试的结果如下:
| 等级 |
优 |
良 |
中 |
不及格 |
| 人数 |
5 |
19 |
23 |
3 |
(1)从该班任意抽取1名学生,求这名学生的测试成绩为“良”或“中”的概率;
(2)测试成绩为“优”的3名男生记为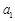 ,
,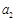 ,
,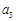 ,2名女生记为
,2名女生记为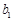 ,
, .现从这5人中任选2人参加学校的某项体育比赛.
.现从这5人中任选2人参加学校的某项体育比赛.
① 写出所有等可能的基本事件;
② 求参赛学生中恰有1名女生的概率.
已知幂函数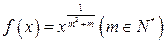
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若函数还经过 ,试确定
,试确定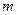 的值,并求满足
的值,并求满足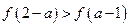 的实数
的实数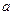 的取值范围。
的取值范围。
某商场经营一批进价是每件30元的商品, 在市场销售中发现此商品的销售单
在市场销售中发现此商品的销售单
价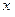 元与日销售量
元与日销售量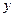 件之间有如下关系:
件之间有如下关系:
销 售单价 售单价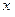 (元) (元) |
30 |
40 |
45 |
50 |
日销售量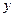 (件) (件) |
60 |
30 |
15 |
0 |
(1)在所给坐标系 中,根据表中提
中,根据表中提 供的数据描出实数对
供的数据描出实数对 对应的点,并确定
对应的点,并确定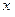 与
与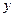 的一个函数关系式
的一个函数关系式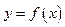 ;
;
(2)设经营此商品的日销售利润为 元,根据上述关系式写出
元,根据上述关系式写出 关于
关于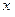 的函数关系式,并指出销售单价
的函数关系式,并指出销售单价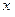 为多少时,才能获得最大日销售利润。
为多少时,才能获得最大日销售利润。
已知集合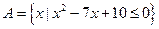 ,
,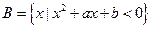 ,且
,且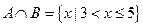 ,
,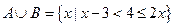 , 求
, 求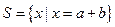 。
。
(本小题满分14分)已知f(x)=ln(1+x)-x.
(Ⅰ)求f(x)的最大值;
(Ⅱ)数列{an}满足:an+1= 2f' (an) +2,且a1=2.5, = bn,
= bn,
⑴数列{ bn+ }是等比数列⑵判断{an}是否为无穷数列。
}是等比数列⑵判断{an}是否为无穷数列。
(Ⅲ)对n∈N*,用⑴结论证明:ln(1+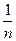 +
+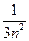 )<
)<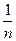 ;
;
(本小题满分13分)已知数列 ,定义其倒均数是
,定义其倒均数是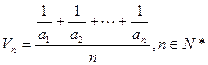 。
。
(1)求数列{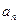 }的倒均数是
}的倒均数是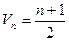 ,求数列{
,求数列{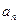 }的通项公式
}的通项公式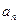 ;
;
(2)设等比数列 的首项为-1,公比为
的首项为-1,公比为 ,其倒数均为
,其倒数均为 ,若存在正整数k,使
,若存在正整数k,使 恒成立,试求k的最小值。
恒成立,试求k的最小值。