(本小题满分14分)在平面直角坐标系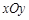 中,已知向量
中,已知向量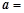 (1,0),
(1,0),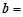 (0,2).设向量
(0,2).设向量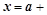 (
( )
)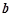 ,
,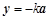
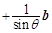 ,其中
,其中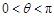 .
.
(1)若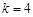 ,
,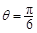 ,求x
,求x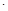 y的值;
y的值;
(2)若x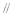 y,求实数
y,求实数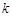 的最大值,并求取最大值时
的最大值,并求取最大值时 的值.
的值.
(本小题满分12分)设{an}是公比为 q的等比数列,且a1,a3,a2成等差数列.
(1)求q的值;
(2)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
(本小题满分12分)若数列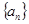 满足前
满足前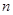 项之和
项之和 且
且 ,
,
(1)求数列 的通项公式
的通项公式
(2)证明: 是等差数列
是等差数列
(3)求 的前
的前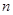 项和
项和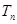 .
.
(本小题满分12分)一变压器的铁芯截面为正十字型,为保证所需的磁通量,要求十字应具有 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽 及长
及长 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
已知a>0,b>0,m>0,n>0,求证:am+n+bm+n ≥ ambn+anbm.
(本题14分)对于函数 ,若
,若 ,则称
,则称 为
为 的“不动点”,若
的“不动点”,若 ,则称
,则称 为
为 的“稳定点”,函数
的“稳定点”,函数 的“不动点”和“稳定点”的集合分别记为A和B,即
的“不动点”和“稳定点”的集合分别记为A和B,即 .
.
(1)设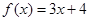 ,求集合A和B;
,求集合A和B;
(2)若 ,
, ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,求证:
,求证: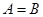 .
.