已知△ABC(如图),∠B=∠C=30度.请设计三种不同的分法,将△ABC分割成四个三角形,使得其中两个是全等三角形,而另外两个是相似但不全等的直角三角形.请画出分割线段,标出能够说明分法的所得三角形的顶点和内角度数(或记号),并在各种分法的空格线上填空.(画图工具不限,不要求证明,不要求写出画法)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.
分法一:
分割后所得的四个三角形中△ DAE ≌△FAE ,Rt△ BDA ∽Rt△ CFE ;
分法二:
分割后所得的四个三角形中△ AFE ≌△BFE ,Rt△ CDA ∽Rt△ BFE ;
分法三:
分割后所得的四个三角形中△ EFD ≌△EFC ,Rt△ BAD ∽Rt△ ADE .
小虫从某点O出发在一直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,各段路程依次为(单位:cm):+5,-3,+10,-8,-6,+12,-13.
(1)小虫最后在出发点O的哪个方向?相距多少厘米?
(2)小虫离出发点O最远是多少厘米?
(3) 在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则小虫一共得到多少粒芝麻?
已知m、x、y满足:(1)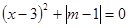 ,(2)
,(2)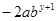 与
与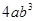 是同类项.求代数式:
是同类项.求代数式: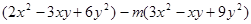 的值.
的值.
如图AB∥DE,∠1=∠2,试说明AE∥DC.下面是解答过程,请你填空或填写理由.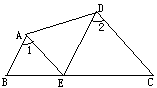
解: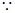 AB∥DE(已知)
AB∥DE(已知)
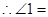 ( )
( )
又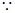 ∠1=∠2 (已知)
∠1=∠2 (已知)
 ∠2= (等量代换)
∠2= (等量代换)
 AE∥DC.( ).
AE∥DC.( ).
如图,这是一个由小立方体搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请你画出它的正视图与左视图.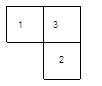
如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度.