如图，已知：△ABC为等边三角形，D、F分别为射线BC、射线AB边上的点，BD=AF，以AD为边作等边△ADE．
（1）如图①所示，当点D在线段BC上时：
①试说明：△ACD≌△CBF；②判断四边形CDEF的形状，并说明理由；
（2）如图②所示，当点D在BC的延长线上时，判断四边形CDEF的形状，并说明理由．
（3）当点D在射线BC上移动到何处时，∠DEF=30°，并说明理由．
如图，∠1=∠2，AB=AD，∠B=∠D，∠3=60º，请判断△AEC的形状，并说明理由。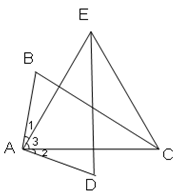
如图，在△ABC中，AB=AC，BD⊥AC，CE⊥AB，O是BD与CE的交点，求证：BO=OC．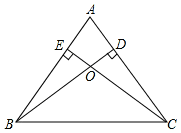
如图，折叠矩形纸片ABCD，先折出折痕（对角线）BD，再折叠AD边与对角线BD重合，得折痕DG，如图所示，若AB=8，BC=6，求AG的长．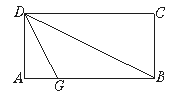
将纸片△ABC沿DE折叠使点A落在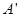
处的位置．
（1）如果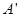落在四边形BCDE的内部（如图1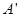），∠与∠1＋∠2之间存在怎样的数量关系？并说明理由．
（2）如果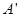落在四边形BCDE的的BE边上，这时图1中的∠1变为0°角，则∠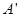与∠2之间的关系是．
（3）如果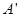落在四边形BCDE的外部（如图2），这时∠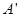与∠1、∠2之间又存在怎样的数量关系？并说明理由．（5+2+5=12分）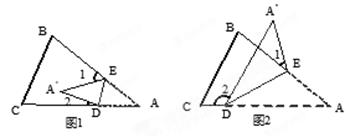
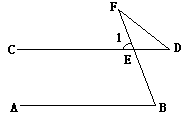
如图，AB∥CD，∠B = 78°，∠D = 32°，求∠F的度数．