(本小题满分15分)已知椭圆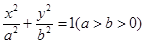 的右焦点
的右焦点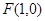 ,离心率为
,离心率为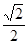 ,过
,过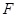 作两条互相垂直的弦
作两条互相垂直的弦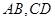 ,设
,设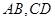 的中点分别为
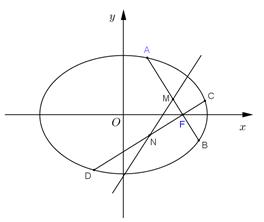
的中点分别为 .
.
(1)求椭圆的方程;
(2)证明:直线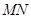 必过定点,并求出此定点坐标;
必过定点,并求出此定点坐标;
(3)若弦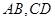 的斜率均存在,求
的斜率均存在,求 面积的最大值.
面积的最大值.
已知 ,
, ,当
,当 为何值时,
为何值时,
(1)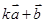 与
与 垂直?(2)
垂直?(2)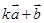 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
在平面直角坐标系中,O为坐标原点,已知向量 ,又点
,又点 ,
,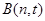 ,
,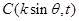 .
.
(1)若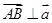 ,且
,且 ,求向量
,求向量 .
.
(2)若向量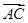 与向量
与向量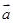 共线,常数
共线,常数 ,当
,当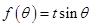 取最大值4时,求
取最大值4时,求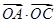 .
.
已知 .
.
(1)求函数 的最小正周期.
的最小正周期.
(2)求函数 在闭区间
在闭区间 上的最小值并求当
上的最小值并求当 取最小值时,
取最小值时,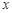 的取值集合.
的取值集合.
已知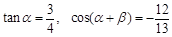 ,且
,且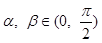 .
.
(1)求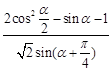 的值; (2)求
的值; (2)求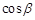 的值.
的值.
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
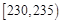 |
8 |
0.16 |
| 第二组 |
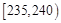 |
① |
0.24 |
| 第三组 |
 |
15 |
② |
| 第四组 |
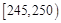 |
10 |
0.20 |
| 第五组 |
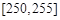 |
5 |
0.10 |
| 合计 |
50 |
1.00 |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.