(本小题满分13分)设知函数 (
( 是自然对数的底数).
是自然对数的底数).
(1)若函数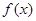 在定义域上不单调,求
在定义域上不单调,求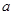 的取值范围;
的取值范围;
(2)设函数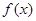 的两个极值点为
的两个极值点为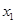 和
和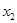 ,记过点
,记过点 ,
, 的直线的斜率为
的直线的斜率为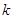 ,是否存在
,是否存在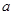 ,使得
,使得 ?若存在,求出
?若存在,求出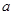 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.
已知函数 (
( 、
、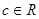 ),满足
),满足 ,且
,且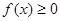 在
在 时恒成立.
时恒成立.
(1)求 、
、 的值;
的值;
(2)若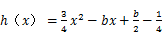 ,解不等式
,解不等式 ;
;
(3)是否存在实数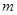 ,使函数
,使函数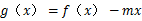 在区间
在区间 上有最小值
上有最小值 ?若存在,请求出
?若存在,请求出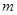 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知函数 的图像与
的图像与 轴正半轴的交点为
轴正半轴的交点为 ,
, =1,2,3,….
=1,2,3,….
求数列 的通项公式;
的通项公式;
令 为正整数), 问是否存在非零整数
为正整数), 问是否存在非零整数 , 使得对任意正整数
, 使得对任意正整数 ,都有
,都有 ? 若存在, 求出
? 若存在, 求出 的值 , 若不存在 , 请说明理由.
的值 , 若不存在 , 请说明理由.
已知
(1)求 的值;
的值;
(2)求 的值.
的值.
如图:三棱锥P-ABC中,PA^底面ABC,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为 .若
.若 是
是 的中点,求:
的中点,求:
(1)三棱锥P-ABC的体积;
(2)异面直线PM与AC所成角的大小(结果用反三角函数值表示).
已知数列 的前
的前 项和
项和 ,则其通项公式为
,则其通项公式为