(本小题12分)六名学生需依次进行身体体能和外语两个项目的训练及考核 每个项目只有一次补考机会,补考不合格者不能进入下一个项目的训练(即淘汰),若每个学生身体体能考核合格的概率是 ,外语考核合格的概率是
,外语考核合格的概率是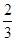 ,假设每一次考试是否合格互不影响.
,假设每一次考试是否合格互不影响.
(1)求某个学生不被淘汰的概率.
(2)求6名学生至多有两名被淘汰的概率
(3)假设某学生不放弃每一次考核的机会,用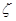 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量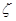 的分布列和数学期望.
的分布列和数学期望.
(本小题满分14分)
已知数列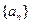 的首项
的首项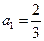 ,
,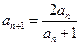 ,
,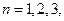 ….
….
(1)证明:数列 是等比数列;
是等比数列;
(2)求数列 的前
的前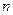 项和
项和 .
.
(本小题满分12分)
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为 ,
, ,
, ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为 ,
, ,
, .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为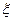 ,求随机变量
,求随机变量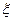 的期望.
的期望.
(本小题满分14分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4, ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.
(1)求证:AC⊥BC1;
(2)求 的体积;
的体积;
(3)求二面角 的平面角的余弦值.
的平面角的余弦值.
已知△ABC的内角A、B、C所对的边分别为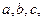 且
且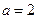 ,
,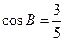 .
.
(1) 若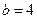 ,求
,求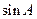 的值;
的值;
(2) 若△ABC的面积 ,求
,求 的值.
的值.
已知函数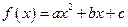
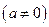 满足
满足 ,对于任意
,对于任意 R都有
R都有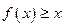 ,且
,且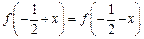 ,令
,令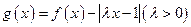 .
.
(1)求函数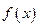 的表达式;
的表达式;
(2)求函数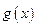 的单调区间;
的单调区间;
(3)研究函数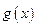 在区间
在区间 上的零点个数.
上的零点个数.