(本小题12分)已知数列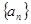 是公差为1的等差数列,
是公差为1的等差数列, 是公比为2的等比数列,
是公比为2的等比数列, 分别是数列
分别是数列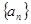 和
和 前n项和,且
前n项和,且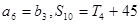
(1)分别求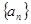 ,
, 的通项公式.
的通项公式.
(2)若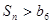 ,求n的范围
,求n的范围
(3)令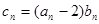 ,求数列
,求数列 的前n项和
的前n项和 .
.
设函数 ,
, ,
,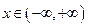 ,且以
,且以 为最小正周期.
为最小正周期.
(1)求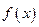 的解析式;
的解析式;
(2)已知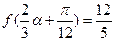 ,求
,求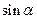 的
的 值.
值.

 已知关于x,y的方程C:
已知关于x,y的方程C: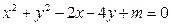 .
.
(1)当m为何值时,方程C表示圆。
(2)若圆C与直线l:x+2y-4=0相交于M,N两点,且MN=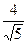 ,求m的值。
,求m的值。
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,AB=5,点D是AB的中点,
(I)求证:AC⊥BC1;(II)求证:AC 1//平面CDB1; 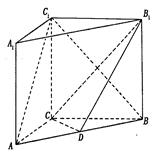
一辆货车的最大载重量为 吨,要装载
吨,要装载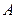 、
、 两种不同的货物,已知装载
两种不同的货物,已知装载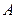 货物每吨收入
货物每吨收入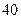 元,装载
元,装载 货物每吨收入
货物每吨收入 元,且要求装载的
元,且要求装载的 货物不少于
货物不少于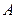 货物的一半.请问
货物的一半.请问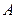 、
、 两种不同的货物分别装载多少吨时,载货得到的收入最大?并求出这个最大值.
两种不同的货物分别装载多少吨时,载货得到的收入最大?并求出这个最大值.
已知:等差数列{ }中,
}中,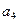 =14,前10项和
=14,前10项和 .
.
(1)求 ;
;
(2)将{ }中的第2项,第4项,…,第
}中的第2项,第4项,…,第 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前 项和
项和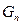 .
.