(本小题满分13分)某小组共有 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2),如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2),如下表所示:
| |
A |
B |
C |
D |
E |
| 身高 |
1.69 |
1.73 |
1.75 |
1.79 |
1.82 |
| 体重指标 |
19.2 |
25.1 |
18.5 |
23.3 |
20.9 |
(Ⅰ)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(Ⅱ)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
(本小题满分14分)
设函数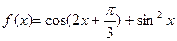 .
.
(I)求f(x)的值域和最小正周期;
(II)设A、B、C为△ ABC的三内角,它们的对边长分别为a、b、c,若cosC=
ABC的三内角,它们的对边长分别为a、b、c,若cosC=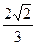 ,A为锐角,且
,A为锐角,且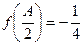 ,
,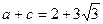 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分15分)
如图已知, 椭圆
椭圆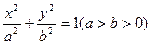 的左、右焦点分别为
的左、右焦点分别为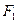 、
、 ,过
,过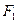 的直线
的直线 与椭圆相交于A、B
与椭圆相交于A、B 两点。
两点。
(Ⅰ)若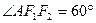 ,且
,且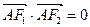 ,求椭圆的离心率;
,求椭圆的离心率;
(Ⅱ)若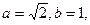 求
求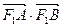 的最大值和最小值。
的最大值和最小值。
(本小题满分15分)
已知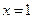 是函数
是函数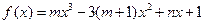 的一个极值点,其中
的一个极值点,其中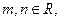
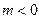 。
。
(Ⅰ)求 与
与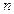 的关系表达式;
的关系表达式;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)当 时,函数
时,函数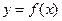 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于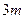 ,求实数
,求实数 的取值范围。
的取值范围。
(本小题满分14分)
设函数
(Ⅰ)若函数的定义域为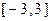 ,求
,求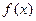 的值域;
的值域;
(Ⅱ)若定义域为[a,a+1]时,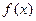 的值域是
的值域是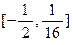 ,求实数a的值。
,求实数a的值。
(本小题满分14分)
已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2、a4的等差中项。
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ,
, ,当
,当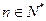 时,
时, 恒成立,试求m的取值范围。
恒成立,试求m的取值范围。