(本小题满分15分)
如图已知, 椭圆
椭圆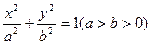 的左、右焦点分别为
的左、右焦点分别为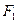 、
、 ,过
,过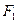 的直线
的直线 与椭圆相交于A、B
与椭圆相交于A、B 两点。
两点。
(Ⅰ)若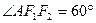 ,且
,且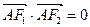 ,求椭圆的离心率;
,求椭圆的离心率;
(Ⅱ)若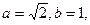 求
求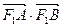 的最大值和最小值。
的最大值和最小值。
如图,已知椭圆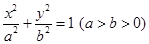 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为
,以该椭圆上的点和椭圆的左右焦点F1、F2为顶点的三角形的周长为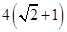 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的焦点分别为A、B和C、D。
(1)求椭圆和双曲线的标准方程
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1
(3)是否存在常数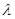 ,使得|AB|+|CD|=
,使得|AB|+|CD|=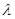 |AB|·|CD|恒成立?
|AB|·|CD|恒成立?
若存在,求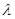 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
已知等差数列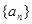 中,公差
中,公差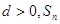 为其前n项和,且满足:
为其前n项和,且满足: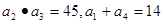 。
。
(1)求数列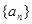 的通项公式;
的通项公式;
(2)通过 构造一个新的数列
构造一个新的数列 ,使
,使 也是等差数列,求非零常数c;
也是等差数列,求非零常数c;
( 3 )求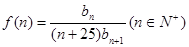 的最大值。
的最大值。
已知三个集合: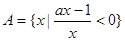 ,
, ,
,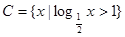 ,同时满足以下三个条件: 甲:
,同时满足以下三个条件: 甲: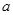 为小于6的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件,试确定数
为小于6的正整数;乙:A是B成立的充分不必要条件;丙:A是C成立的必要不充分条件,试确定数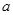 。
。
设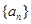 是等差数列,
是等差数列,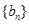 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且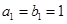 ,
,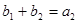 ,
, 。
。
(1)求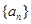 ,
,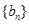 的通项公式;
的通项公式;
(2)求数列 的前n项和
的前n项和 .
.
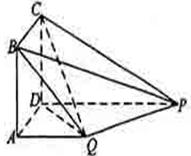
如图,四边形ABCD为正方形,PD⊥平面ABCD ,PD∥QA,QA=AB=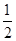 PD.
PD.
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q—BP—C的正弦值.