(本小题满分13分)设数列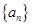 满足:
满足:
① ;
;
②所有项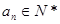 ;
;
③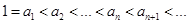 .
.
设集合 ,将集合
,将集合 中的元素的最大值记为
中的元素的最大值记为 ,即
,即 是数列
是数列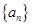 中满足不等式
中满足不等式 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列 为数
为数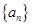 的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(Ⅰ)若数列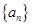 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列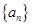 ;
;
(Ⅱ)设 ,求数列
,求数列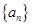 的伴随数列
的伴随数列 的前30项之和;
的前30项之和;
(Ⅲ)若数列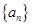 的前
的前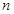 项和
项和 (其中
(其中 常数),求数列
常数),求数列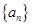 的伴随数列
的伴随数列
的前 项和
项和 .
.
某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定.他们三人都有“同意”、“中立”、“反对”三类票各一张.投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为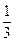 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.
(Ⅰ)求此公司决定对该项目投资的概率;
(Ⅱ)记投票结果中“中立”票的张数为随机变量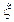 ,求
,求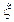 的分布列及数学期望E
的分布列及数学期望E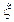 .
.
设全集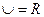 ,函数
,函数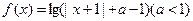 的定义域为A,集合
的定义域为A,集合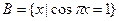 ,若
,若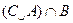 恰好有2个元素,求a的取值集合。
恰好有2个元素,求a的取值集合。
已知函数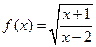 的定义域集合是A,
的定义域集合是A,
函数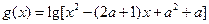 的定义域集合是B(1)求集合A、B(2)若A
的定义域集合是B(1)求集合A、B(2)若A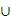 B=B,求实数
B=B,求实数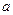 的取值范围.
的取值范围.
集合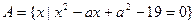 ,
,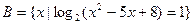 ,
,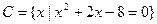 ,求a的值使
,求a的值使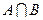 Æ,且
Æ,且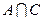 =Æ同时成立。
=Æ同时成立。
如图6,正方形ABCD所在平面与三角形CDE所在平面ABCD相交于CD,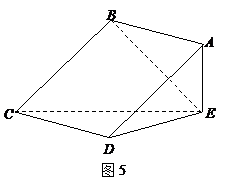
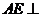 平面CDE,且
平面CDE,且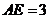 ,
,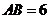 .
.
(1)求证: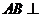 平面
平面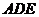 ;
;
(2)求凸多面体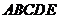 的体积.
的体积.