（本小题满分12分）将一个半径适当的小球放入如图所示的容器最上方的入口处，小球自由下落，小球在下落的过程中，将遇到黑色障碍物
次，最后落入
袋或
袋中．已知小球每次遇到障碍物时，向左、右两边下落的概率分别是
（Ⅰ）分别求出小球落入袋和袋中的概率；
（Ⅱ）在容器的入口处依次放入
个小球，记
为落入袋中的小球个数，求的分布列和数学期望．
为防止山体滑坡，某地决定建设既美化又防护的绿化带，种植松树、柳树等植物．某人一次种植了n株柳树，各株柳树成活与否是相互独立的，成活率为p，设ξ为成活柳树的株数，数学期望E(ξ)＝3，标准差σ(ξ)为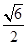
.
(1)求n、p的值并写出ξ的分布列；
(2)若有3株或3株以上的柳树未成活，则需要补种，求需要补种柳树的概率．
设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分．
(1)当a＝3，b＝2，c＝1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量ξ为取出此两球所得分数之和，求ξ分布列；
(2)从该袋子中任取(且每球取到的机会均等)1个球，记随机变量η为取出此球所得分数．若E(η)＝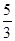
，V(η)＝
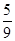，求a∶b∶c.
甲、乙两名射手在一次射击中的得分为两个相互独立的随机变量ξ和η，且ξ、η分布列为
| ξ |
1 |
2 |
3 |
| P |
a |
0.1 |
0.6 |
| η |
1 |
2 |
3 |
| P |
0.3 |
b |
0.3 |
(1)求a、b的值；
(2)计算ξ、η的期望和方差，并以此分析甲、乙的技术状况．
某电器商经过多年的经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量，它的分布列为P(ξ＝i)＝
(i＝1，2，…，12)；设每售出一台电冰箱，电器商获利300元．如销售不出，则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大？
一盒中装有零件12个，其中有9个正品，3个次品，从中任取一个，如果每次取出次品就不再放回去，再取一个零件，直到取得正品为止．求在取得正品之前已取出次品数的期望．