如图,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.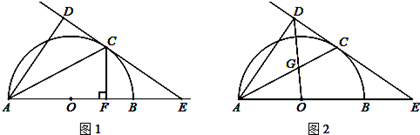
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图2,连接OD交AC于点G,若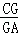 =
=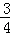 ,求sin∠E的值.
,求sin∠E的值.
(本题7分)阅读下列材料:
一般地,n个相同的因数a相乘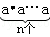 记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算以下各对数的值:
log24=,log216=,log264=.
(2)观察(1)中三数4、16、64之间满足怎样的关系式,log24、log216、log264之间又满足怎样的关系式;
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN=;(a>0且a≠1,M>0,N>0)
(4)根据幂的运算法则:an•am=an+m以及对数的含义说明上述结论成立.
已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,则∠ABD+∠ACD=度;
(2)当将△DEF如图2摆放时,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论.(填“能”或“不能”)
(本题7分)下面是某同学对多项式( -4x+2)(
-4x+2)( -4x+6)+4进行因式分解的过程.
-4x+6)+4进行因式分解的过程.
解:设x-4x=y,
原式=(y+2)(y+6)+4(第一步)
= +8y+16(第二步)
+8y+16(第二步)
= (第三步)
(第三步)
=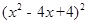 (第四步)
(第四步)
请问:
(1)该同学因式分解的结果是否彻底?____________。(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果____________________________;
(2)请你模仿以上方法尝试对多项式(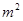 -2m)(
-2m)(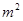 -2m+2)+1进行因式分解.
-2m+2)+1进行因式分解.
(本题6分)如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。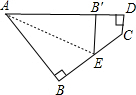
(1)试判断B'E与DC的位置关系并说明理由;
(2)如果∠C=130°,求∠AEB的度数。
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.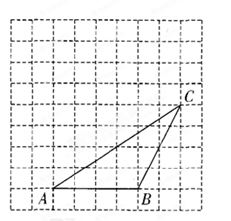
(1)请在图中画出平移后的△A´B´C´,
(2)再在图中画出△ABC的高CD,
(3)在右图中能使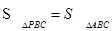 的格点P的个数有 个(点P异于A).
的格点P的个数有 个(点P异于A).