(本小题满分14分)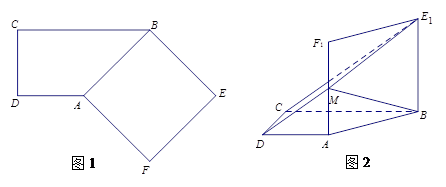
如图1,在直角梯形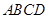 中,
中,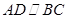 ,
, ,
, ,四边形
,四边形 是正方形.将正方形
是正方形.将正方形 沿
沿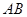 折起到四边形
折起到四边形 的位置,使平面
的位置,使平面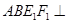 平面
平面 ,
,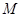 为
为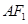 的中点,如图2.
的中点,如图2.
(1)求证: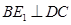 ;
;
(2)求 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)判断直线 与
与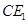 的位置关系,并说明理由.
的位置关系,并说明理由.
某地区1997年底沙漠面积为 hm
hm .地质工作者为了解这个地区沙漠面积的变化情况,从1998年开始进行了连续5年的观测,并在每年底将观测结果记录如下表:
.地质工作者为了解这个地区沙漠面积的变化情况,从1998年开始进行了连续5年的观测,并在每年底将观测结果记录如下表:
| 观测年份 |
该地区沙漠面积比原有面积增加数 hm  |
| 1998 |
2000 |
| 1999 |
4000 |
| 2000 |
6001 |
| 2001 |
7999 |
| 2002 |
10001 |
请根据上表所给的信息进行预测.
(1)如果不采取任何措施,到2010年底,这个地区的沙漠面积将大约变成多少hm ?
?
(2)如果从2003年初开始,采取植树造林等措施,每年改造8000 hm 沙漠,但沙漠面积仍按原有速度增加,那么到哪一年年底,这个地区的沙漠面积将小于
沙漠,但沙漠面积仍按原有速度增加,那么到哪一年年底,这个地区的沙漠面积将小于 hm
hm ?
?
标有1,2,3,4,5,6六个号码的小球,有一个最重,写出挑出此重球的算法并画出程序框图.
已知数列 的前
的前 项和为
项和为 ,求这个数列的通项公式.这个数列是等差数列吗?如果是,它的首项与公差分别是什么?
,求这个数列的通项公式.这个数列是等差数列吗?如果是,它的首项与公差分别是什么?
已知等差数列 的前
的前 项和为
项和为 ,求使得
,求使得 最大的序号
最大的序号 的值.
的值.
某市出租车的计价标准为 元/km,起步价为10元,即最初的4km(不含4千米)计费10元.如果某人乘坐该市的出租车去往14 km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?
元/km,起步价为10元,即最初的4km(不含4千米)计费10元.如果某人乘坐该市的出租车去往14 km处的目的地,且一路畅通,等候时间为0,需要支付多少车费?