(本小题满分13分)在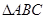 中,
中, .
.
(Ⅰ)若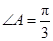 ,求
,求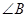 的大小;
的大小;
(Ⅱ)若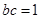 ,求
,求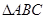 的面积的最大值.
的面积的最大值.
已知函数
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明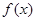 在
在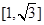 上是增函数;
上是增函数;
(Ⅲ)求出函数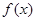 在
在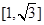 的最值.
的最值.
设集合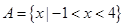 ,
,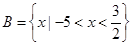 ,
,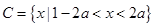 .
.
(Ⅰ)若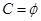 ,求实数
,求实数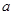 的取值范围;(Ⅱ)若
的取值范围;(Ⅱ)若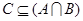 ,求实数
,求实数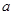 的取值范围.
的取值范围.
设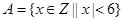 ,
,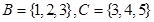 ,求:
,求:
(Ⅰ)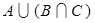 ;(Ⅱ)
;(Ⅱ)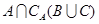
(本小题只理科做,满分14分)如图,已知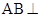 平面
平面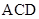 ,
,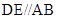 ,△
,△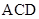 是正三角形,
是正三角形,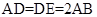 ,且
,且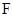 是
是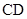 的中点.
的中点.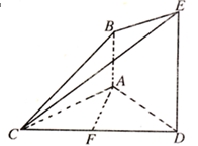
(1)求证: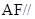 平面
平面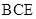 ;
;
(2)求证:平面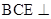 平面
平面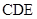 ;
;
(3)求平面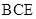 与平面
与平面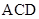 所成锐二面角的大小.
所成锐二面角的大小.
(本小题文科14分理科13分).某公司今年初用25万元引进一种新的设备,设备投入运行后,每年销售收入为21万元。已知该公司第n年需要付出设备的维修和工人工资等费用的和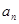 的信息如下图。
的信息如下图。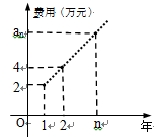
(1)求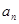 ;
;
(2)该公司引进这种设备后,第几年后开始获利、第几年后开始亏损?
(3)这种设备使用多少年,该公司的年平均获利最大?(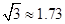 )
)