(本小题满分13分)某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下: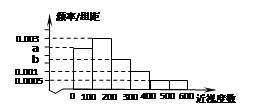
| 近视度数 |
0–100 |
100–200 |
200–300 |
300–400 |
400以上 |
| 学生频数 |
30 |
40 |
20 |
10 |
0 |
将近视程度由低到高分为4个等级:当近视度数在0-100时,称为不近视,记作0;当近视度数在100-200时,称为轻度近视,记作1;当近视度数在200-400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设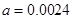 ,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量 分别表示高二、高三年级学生的近视程度,若
分别表示高二、高三年级学生的近视程度,若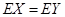 ,求
,求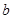 .
.