(本小题满分12分)已知椭圆 :
: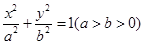 的上顶点为
的上顶点为 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)证明:过椭圆 :
: 上一点
上一点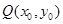 的切线方程为
的切线方程为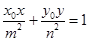 ;
;
(3)从圆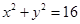 上一点
上一点 向椭圆
向椭圆 引两条切线,切点分别为
引两条切线,切点分别为 ,
, ,当直线
,当直线 分别与
分别与 轴,
轴, 轴交于
轴交于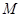 ,
, 两点时,求
两点时,求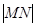 的最小值.
的最小值.
如图所示,空间中有一直角三角形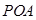 ,
, 为直角,
为直角,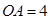 ,
,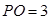 ,现以其中一直角边
,现以其中一直角边 为轴,按逆时针方向旋转
为轴,按逆时针方向旋转 后,将
后,将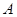 点所在的位置记为
点所在的位置记为 ,再按逆时针方向继续旋转
,再按逆时针方向继续旋转 后,
后,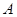 点所在的位置记为
点所在的位置记为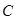 .
.
(1)连接 ,取
,取 的中点为
的中点为 ,求证:面
,求证:面 面
面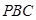 ;
;
(2)求 与平面
与平面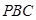 所成的角的正弦值.
所成的角的正弦值.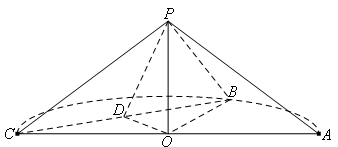
如图所示,某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料,已知已有两面墙 、
、 的夹角为
的夹角为 (即
(即 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 米),为了使得仓库的面积尽可能大,记
米),为了使得仓库的面积尽可能大,记 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 
如图,一半径为 的圆形靶内有一个半径为
的圆形靶内有一个半径为 的同心圆,将大圆分成两
的同心圆,将大圆分成两
部分,小圆内部区域记为 环,圆环区域记为
环,圆环区域记为 环,某同学向该靶投掷
环,某同学向该靶投掷 枚飞镖,每次
枚飞镖,每次 枚. 假设他每次必
枚. 假设他每次必
定会中靶,且投中靶内各点是随机的.
(1)求该同学在一次投掷中获得 环的概率;
环的概率;
(2)设 表示该同学在
表示该同学在 次投掷中获得的环数,求
次投掷中获得的环数,求 的分布列及数学期望.
的分布列及数学期望.
已知函数 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)当 时,函数
时,函数 图象上的点都在
图象上的点都在 所表示的平面区域内,不等式
所表示的平面区域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知抛物线 上有一点
上有一点 到焦点
到焦点 的距离为
的距离为 .
.
(1)求 及
及 的值.
的值.
(2)如图,设直线 与抛物线交于两点
与抛物线交于两点 ,且
,且 ,过弦
,过弦 的中点
的中点 作垂直于
作垂直于 轴的直线与抛物线交于点
轴的直线与抛物线交于点 ,连接
,连接 .试判断
.试判断 的面积是否为定值?若是,求出定值;否则,请说明理由.
的面积是否为定值?若是,求出定值;否则,请说明理由. 