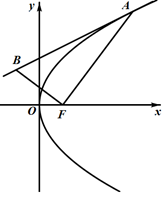
如图所示,抛物线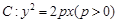 与直线
与直线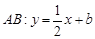 相切于点
相切于点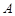 .
.
(1)求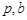 满足的关系式,并用
满足的关系式,并用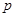 表示点
表示点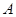 的坐标;
的坐标;
(2)设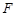 是抛物线的焦点,若以
是抛物线的焦点,若以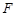 为直角顶角的
为直角顶角的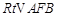 的面积等于
的面积等于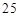 ,求抛物线
,求抛物线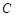 的标准方程.
的标准方程.
已知椭圆 :
: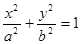
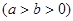 ,
,
(1)若椭圆的长轴长为4,离心率为 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)在(1)的条件下,设过定点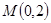 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点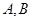 ,且
,且 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率 的取值范围;
的取值范围;
(3)过原点 任意作两条互相垂直的直线与椭圆
任意作两条互相垂直的直线与椭圆 :
: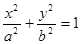
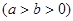 相交于
相交于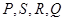 四点,设原点
四点,设原点 到四边形
到四边形 的一边距离为
的一边距离为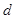 ,试求
,试求 时
时 满足的条件.
满足的条件.
已知函数 ,
,
(1)求函数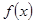 的极值点;
的极值点;
(2)若直线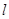 过点
过点 ,并且与曲线
,并且与曲线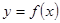 相切,求直线
相切,求直线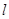 的方程;
的方程;
(3)设函数 ,其中
,其中 ,求函数
,求函数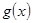 在
在 上的最小值(其中
上的最小值(其中 为自然对数的底数).
为自然对数的底数).
某品牌汽车的4 店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4
店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4 店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用
店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用 表示经销一辆该品牌汽车的利润.
表示经销一辆该品牌汽车的利润.
| 付款方式 |
一次 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频数 |
40 |
20 |
a |
10 |
b |
(1)若以频率作为概率,求事件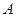 :“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率 ;
;
(2)求 的分布列及其数学期望
的分布列及其数学期望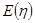 .
.
如图所示,正方形 与矩形
与矩形 所在平面互相垂直,
所在平面互相垂直, ,点
,点 为
为 的中点.
的中点.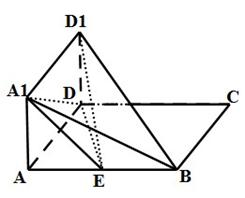
(1)求证: ∥平面
∥平面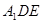 ;
;
(2)求证: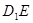
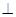
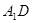 ;
;
(3)在线段 上是否存在点
上是否存在点 ,使二面角
,使二面角 的大小为
的大小为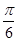 ?若存在,求出
?若存在,求出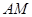 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
在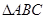 中,已知
中,已知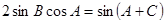
(1)求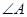 ;
;
(2)若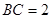 ,
,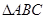 的面积是
的面积是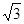 ,求
,求 .
.