【选修4—2:矩阵与变换】(本小题满分10分)
已知矩阵M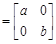 ,若直线
,若直线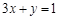 在矩阵M对应的变换作用下得到直线
在矩阵M对应的变换作用下得到直线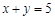 ,求矩阵M的特征值.
,求矩阵M的特征值.
(本小题满分12分)已知直线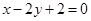 经过椭圆
经过椭圆 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆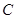 的右顶点为
的右顶点为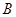 ,点
,点 和椭圆
和椭圆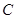 上位于
上位于 轴上方的动点,直线,
轴上方的动点,直线, 与直线
与直线 分别交于
分别交于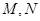 两点。
两点。
(I)求椭圆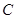 的方程;
的方程;
(Ⅱ)求线段MN的长度的最小值;
(Ⅲ)当线段MN的长度最小时,在椭圆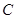 上是否存在这
上是否存在这
样的点 ,使得
,使得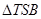 的面积为
的面积为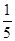 ?若存在,确定点
?若存在,确定点 的个数,若不存在,说明理由
的个数,若不存在,说明理由
(本小题满分12分)己知函数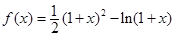
(1)求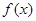 的单调区间;
的单调区间;
(2)若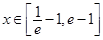 时,
时,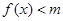 恒成立,求
恒成立,求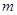 的取值范围;
的取值范围;
(3)若设函数 ,若
,若 的图象与
的图象与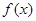 的图象在区间
的图象在区间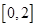 上有两个交点,求
上有两个交点,求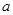 的取值范围。
的取值范围。
(本小题满分12分)
等比数列{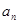 }的前n项和为
}的前n项和为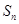 , 已知对任意的
, 已知对任意的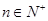 ,点
,点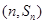 ,均在函数
,均在函数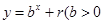 且
且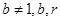 均为常数)的图像上.
均为常数)的图像上.
(1)求r的值;
(2)当b=2时,记 求数列
求数列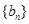 的前
的前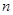 项和
项和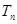
(本小题满分12分)
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.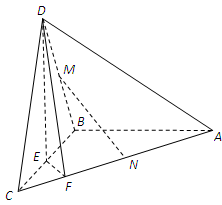
(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.
(本小题满分12分)某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(1)求每个报名者能被聘用的概率;
(2)随机调查了24名笔试者的成绩如下表所示:
| 分数段 |
[60,65) |
[65,70) |
[70,75) |
[75,80) |
[80,85) |
[85,90) |
| 人数 |
1 |
2 |
6 |
9 |
5 |
1 |
请你预测面试的分数线大约是多少?
(3)公司从聘用的四男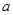 、
、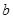 、
、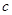 、
、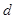 和二女
和二女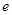 、
、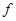 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少?