（本小题满分14分）如图，已知椭圆
：
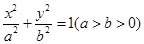的离心率为
， 
、
、
、
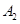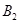是其四个顶点，且四边形
的面积为
．
（Ⅰ）求椭圆的方程；
（Ⅱ）已知直线
与椭圆交于
、
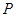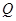两点，
（ⅰ）若直线过点
，则是否存在直线，使得以
为直径的圆经过点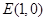
？求直线的方程；如果存在求出直线的方程；如果不存在，是说明理由．
（ⅱ）若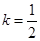
，且坐标原点在以为直径的圆外，求该直线在
轴上的截距的取值范围．
已知中心在坐标原点O的椭圆C经过点A（2，3），且点F（2，0）为其右焦点
（1）求椭圆C的方程；
（2）是否存在平行于OA的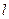直线
，使得直线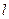与椭圆C有公共点，且直线OA与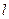的距离等于4？若存在，求出直线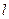的方程；若不存在，请说明理由。
某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
| 零件的个数x(个） |
2 |
3 |
4 |
5 |
| 加工的时间y(小时） |
2.5 |
3 |
4 |
4.5 |
（1）在给定的坐标系中画出表中数据的散点图
（2）求出y关于x的线性回归方程；
（3）试预测加工10个零件需要多长时间？
某研究机构为了研究人的脚的大小（码）与身高（厘米）之间的关系，随机抽测了20人，得到如下数据：
| 序号 |
身高x |
脚长y |
序号 |
身高x |
脚长y |
| 1 |
176 |
42 |
11 |
179 |
44 |
| 2 |
175 |
44 |
12 |
169 |
43 |
| 3 |
174 |
41 |
13 |
185 |
45 |
| 4 |
180 |
44 |
14 |
166 |
40 |
| 5 |
170 |
42 |
15 |
174 |
42 |
| 6 |
178 |
43 |
16 |
167 |
42 |
| 7 |
173 |
42 |
17 |
173 |
41 |
| 8 |
168 |
40 |
18 |
174 |
42 |
| 9 |
190 |
46 |
19 |
172 |
42 |
| 10 |
171 |
42 |
20 |
175 |
41 |
(1)若“身高大于175厘米”的为“高个”，“身高小于等于175厘米”的为“非高个”，“脚长大于42码”的为“大脚”，“脚长小于等于42码”的为“非大脚”.请根据上表数据完成如下2×2列联表；
| 高个 |
非高个 |
合计 |
|
| 大脚 |
|||
| 非大脚 |
12 |
||
| 合计 |
20 |
（2）根据题（1）中表格的数据，若按99%的可靠性要求，能否认为脚的大小与身高有关系？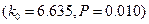 
已知数列
中，
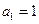，且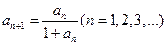
，
（1）试归纳出这个数列的通项公式；(不用证明)
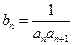（2）设数列
，求数列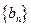
的前n项和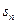
.
已知函数
,若函数
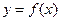在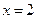
处有极值-6，求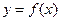的单调递减区间；