图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m).(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
|
阅读时间 (小时) |
频数 (人 |
频率 |
|
|
18 |
0.12 |
|
|
|
|
|
|
45 |
0.3 |
|
|
36 |
|
|
|
21 |
0.14 |
|
合计 |
|
1 |
(1)填空: , , , ;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由3000名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.

如图,一次函数 的图象与反比例函数 的图象交于 , 两点,且点 的横坐标为3.
(1)求反比例函数的解析式;
(2)求点 的坐标.

尺规作图(不写作法,保留作图痕迹)
已知线段 和 ,点 在 上(如图所示).
(1)在 边上作点 ,使 ;
(2)作 的平分线;
(3)过点 作 的垂线.

如图,已知抛物线 与坐标轴交于 , , 三点,其中 , 的平分线 交 轴于点 ,交 于点 ,过点 的直线 与射线 , 分别交于点 , .
(1)直接写出 的值、点 的坐标及抛物线的对称轴;
(2)点 为抛物线的对称轴上一动点,若 为等腰三角形,求出点 的坐标;
(3)证明:当直线 绕点 旋转时, 均为定值,并求出该定值.

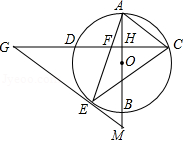
如图, 是 的直径,弦 ,垂足为 ,连接 ,过 上一点 作 交 的延长线于点 ,连接 交 于点 ,且 ,连接 .
(1)求证: ;
(2)求证: 是 的切线;
(3)延长 交 的延长线于点 ,若 , ,求 的值.