尺规作图(不写作法,保留作图痕迹)
已知线段 和 ,点 在 上(如图所示).
(1)在 边上作点 ,使 ;
(2)作 的平分线;
(3)过点 作 的垂线.

已知二次函数 y= ax 2﹣ bx+ c且 a= b,若一次函数 y= kx+4与二次函数的图象交于点 A(2,0).
(1)写出一次函数的解析式,并求出二次函数与 x轴交点坐标;
(2)当 a> c时,求证:直线 y= kx+4与抛物线 y= ax 2﹣ bx+ c一定还有另一个异于点 A的交点;
(3)当 c< a≤ c+3时,求出直线 y= kx+4与抛物线 y= ax 2﹣ bx+ c的另一个交点 B的坐标;记抛物线顶点为 M,抛物线对称轴与直线 y= kx+4的交点为 N,设 S= S △ AMN﹣ S △ BMN,写出 S关于 a的函数,并判断 S是否有最大值?如果有,求出最大值;如果没有,请说明理由.
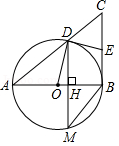
如图,以Rt△ ABC的直角边 AB为直径的⊙ O交斜边 AC于点 D,过点 D作⊙ O的切线与 BC交于点 E,弦 DM与 AB垂直,垂足为 H.
(1)求证: E为 BC的中点;
(2)若⊙ O的面积为12π,两个三角形△ AHD和△ BMH的外接圆面积之比为3,求△ DEC的内切圆面积 S 1和四边形 OBED的外接圆面积 S 2的比.
如图,在平面直角坐标系中,矩形 OCAB( OC> OB)的对角线长为5,周长为14.若反比例函数 y= 的图象经过矩形顶点 A.
(1)求反比例函数解析式;若点(﹣ a, y 1)和( a+1, y 2)在反比例函数的图象上,试比较 y 1与 y 2的大小;
(2)若一次函数 y= kx+ b的图象过点 A并与 x轴交于点(﹣1,0),求出一次函数解析式,并直接写出 kx+ b﹣ <0成立时,对应 x的取值范围.

滴滴快车是一种便捷的出行工具,计价规则如下表:
|
计费项目 |
里程费 |
时长费 |
远途费 |
|
单价 |
1.8元/公里 |
0.3元/分钟 |
0.8元/公里 |
|
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元. |
|||
小王与小张各自乘坐满滴快车,在同一地点约见,已知到达约见地点时他们的实际行车里程分别为6公里与8.5公里,两人付给滴滴快车的乘车费相同.
(1)求这两辆滴滴快车的实际行车时间相差多少分钟;
(2)实际乘车时间较少的人,由于出发时间比另一人早,所以提前到达约见地点在大厅等候.已知他等候另一人的时间是他自己实际乘车时间的1.5倍,且比另一人的实际乘车时间的一半多8.5分钟,计算俩人各自的实际乘车时间.
镇政府想了解对王家村进行"精准扶贫"一年来村民的经济情况,统计员小李用简单随机抽样的方法,在全村130户家庭中随机抽取20户,调查过去一年的收入(单位:万元),从而去估计全村家庭年收入情况.
已知调查得到的数据如下:
1.9,1.3,1.7,1.4,1.6,1.5,2.7,2.1,1.5,0.9,2.6,2.0,2.1,1.0,1.8,2.2,2.4,3.2,1.3,2.8
为了便于计算,小李在原数据的每个数上都减去1.5,得到下面第二组数:
0.4,﹣0.2,0.2,﹣0.1,0.1,0,1.2,0.6,0,﹣0.6,1.1,0.5,0.6,﹣0.5,0.3,0.7,0.9,1.7,﹣0.2,1.3
(1)请你用小李得到的第二组数计算这20户家庭的平均年收入,并估计全村年收入及全村家庭年收入超过1.5万元的百分比;已知某家庭过去一年的收入是1.89万元,请你用调查得到的数据的中位数推测该家庭的收入情况在全村处于什么水平?
(2)已知小李算得第二组数的方差是 S,小王依据第二组数的方差得出原数据的方差为(1.5+ S) 2,你认为小王的结果正确吗?如果不正确,直接写出你认为正确的结果.