有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B 布袋中有三个完全相同的小球，分别标有数字-1，-2和-3．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为
．
（1）用列表或画树状图的方法写出点Q的所有可能坐标；
（2）求点Q落在抛物线y=x2-2x-1上的概率．
有一个不透明口袋，装有分别标有数字1，2，3，4的4个小球（小球除数字不同外，其余都相同），另有3张背面完全一样、正面分别写有数字1，2，3的卡片．小敏从口袋中任意摸出一个小球，小颖从这3张背面朝上的卡片中任意摸出一张，然后计算小球和卡片上的两个数的积．
（1）请你用列表或画树状图的方法，求摸出的这两个数的积为6的概率；
（2）小敏和小颖做游戏，她们约定：若这两个数的积为奇数，小敏赢；否则，小颖赢．你认为该游戏公平吗？为什么？如果不公平，请你修改游戏规则，使游戏公平．
如图，点E是正方形ABCD的边AB上任意一点，过点D作DF⊥DE交BC的延长线于点F．求证：DE=DF．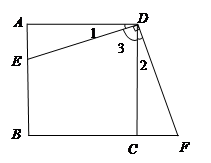
(6分)如图所示，某幼儿园有一道长为16米的墙，计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD．求该矩形草坪BC边的长．
如图1，在平面直角坐标系中，
为坐标原点.直线
与抛物线
同时经过
.
（1）求
的值.
（2）点
是二次函数图象上一点，(点在
下方)，过作
轴，与交于点
，与轴交于点
.求
的最大值.
（3）在（2）的条件下，是否存在点,使
和 
相似？若存在，求出点坐标，不存在，说明理由.
中，AB=AC，将线段AB绕点A按逆时针方向旋转
得到线段AD,其中
.连结BD，CD， 
.
（1）若
，
,在图1中补全图形，并写出m值.
（2）如图2，当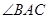
为钝角，
时 ，
值是否发生改变？证明你的猜想.
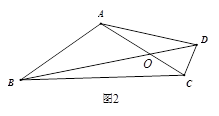
(3) 如图3，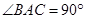
，
，BD与AC相交于点O，求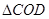
与
的面积比.