(本小题满分10分)选修4-4:极坐标系与参数方程
已知极坐标系与直角坐标系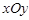 有相同的长度单位,以原点
有相同的长度单位,以原点 为极点,以
为极点,以 正半轴为极轴,已知曲线
正半轴为极轴,已知曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线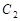 的参数方程是
的参数方程是 (
( 为参数,
为参数,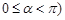 ,射线
,射线 与曲线
与曲线 交于极点
交于极点 外的三点
外的三点
(1)求证: ;
;
(2)当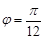 时,
时, 两点在曲线
两点在曲线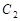 上,求
上,求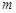 与
与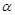 的值.
的值.
(本小题满分14分)已知函数 ,其中
,其中 为实数.
为实数.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ) 当 时,若函数
时,若函数 对定义域内的任意
对定义域内的任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(Ⅲ)证明,对于任意的正整数 ,不等式
,不等式 恒成立.
恒成立.
(本小题满分12分)如图,在平面直角坐标系 中,离心率为
中,离心率为 的椭圆
的椭圆
 的左顶点为
的左顶点为 ,过原点
,过原点 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于 两点,直线
两点,直线 分别与
分别与 轴交于
轴交于 两点.若直线
两点.若直线 斜率为
斜率为 时,
时, .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)试问以 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
(本小题满分12分)如图,在四棱锥 中,
中, ,
, 平面
平面 ,
,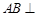 平面
平面 ,
,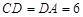 ,
,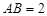 ,
,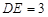 .
.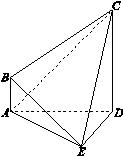
(Ⅰ)求棱锥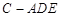 的体积;
的体积;
(Ⅱ)求证:平面
 平面
平面 ;
;
(Ⅲ)在线段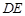 上是否存在一点
上是否存在一点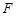 ,使
,使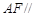 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分12分)在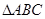 中,内角
中,内角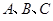 的对边分别为
的对边分别为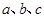 ,
,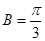 .
.
(Ⅰ)若 ,
, ,求
,求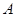 和
和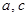 ;
;
(Ⅱ) 若 ,且
,且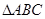 的面积为2
的面积为2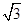 ,求
,求 的大小.
的大小.
(本小题满分12分)某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为 ,
, ,
, ,
, ,
, .
.
(Ⅰ)求频率分布直方图中 的值;
的值;
(Ⅱ)从统计学的角度说明学校是否需要推迟5分钟上课;
(Ⅲ)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在 上的概率.
上的概率.