(本小题满分12分)如图,三角形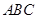 中,
中,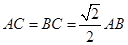 ,
, 是边长为
是边长为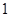 的正方形,平面
的正方形,平面 ⊥平面
⊥平面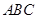 ,若
,若 分别是
分别是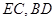 的中点.
的中点.
(1)求证: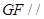 平面
平面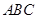 ;
;
(2)求证: ⊥平面
⊥平面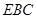 ;
;
(3)求几何体 的体积.
的体积.
证明:若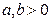 ,则
,则
我们将具有下列性质的所有函数组成集合M:函数 ,对任意
,对任意 均满足
均满足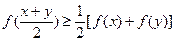 ,当且仅当
,当且仅当 时等号成立。
时等号成立。
(1)若定义在(0,+∞)上的函数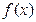 ∈M,试比较
∈M,试比较 与
与 大小.
大小.
(2)设函数g(x)=-x2,求证:g(x)∈M.
已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)=T f(x)成立.
(1)函数f(x)= x是否属于集合M?说明理由;
(2)设函数f(x)=ax(a>0,且a≠1)的图象与y=x的图象有公共点,证明:f(x)=ax∈M;
(3)若函数f(x)=sinkx∈M ,求实数k的取值范围.
在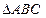 中,若
中,若 ,则
,则 ,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
通过观察下列等式,猜想出一个一般性的结论,并证明结论的真假。 ;
; ;
;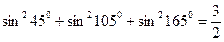 ;
;