问题1：在图1中，已知线段AB，CD，它们的中点分别为E，F．
①若
，
，则
点坐标为_____________；
②若
，
，则
点坐标为____________；
问题2：在图2中，无论线段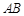
处于直角坐标系中的哪个位置，当其端点坐标为
，
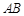，中
点为
时，请直接写出
点的坐标（____________，___________）；（用含
、
、
、
的式子表示）．
问题3：如图3，一次函数
与反比例函数
的图象交于
、
两点，若以、
、、
为顶
点的四边形是平行四边形，请直接写出顶点的坐标______________．
先化简，再求值： ，其中 ．
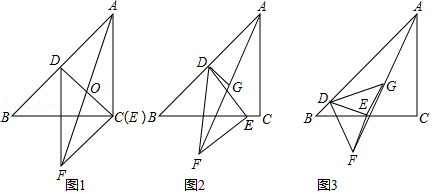
如图，在等腰 中， ， ，点 ， 分别在边 ， 上，将线段 绕点 按逆时针方向旋转 得到 ．
（1）如图1，若 ，点 与点 重合， 与 相交于点 ．求证： ．
（2）已知点 为 的中点．
①如图2，若 ， ，求 的长．
②若 ，是否存在点 ，使得 是直角三角形？若存在，求 的长；若不存在，试说明理由．
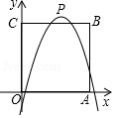
如图，在平面直角坐标系中，正方形 的边长为4，边 ， 分别在 轴， 轴的正半轴上，把正方形 的内部及边上，横、纵坐标均为整数的点称为好点．点 为抛物线 的顶点．
（1）当 时，求该抛物线下方（包括边界）的好点个数．
（2）当 时，求该抛物线上的好点坐标．
（3）若点 在正方形 内部，该抛物线下方（包括边界）恰好存在8个好点，求 的取值范围．
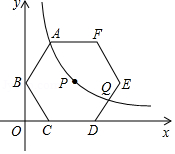
如图，在平面直角坐标系中，正六边形 的对称中心 在反比例函数 的图象上，边 在 轴上，点 在 轴上，已知 ．
（1）点 是否在该反比例函数的图象上？请说明理由；
（2）若该反比例函数图象与 交于点 ，求点 的横坐标；
（3）平移正六边形 ，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．
如图，在 中，以 为圆心， 为半径的圆与 相切于点 ，与 相交于点 ．
（1）求 的度数．
（2）如图，点 在 上，连结 与 交于点 ，若 ，求 的度数．
