已知二次函数y=（t-4）x2-（2t-5）x+4在x=0与x=5的函数值相等．
（1）求二次函数的解析式；
（2）若二次函数的图象与x轴交于A，B两点（A在B左侧），与y轴交于点C，一次函数y=kx+b经过B，C两点，求一次函数的表达式；
（3）在（2）的条件下，过动点D（0，m） 作直线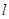
//x轴，其中
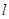．将二次函数图象在直线下方的部分沿直线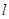向上翻折，其余部分保持不变，得到一个新图象M．若直线
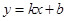与新图象M恰有两个公共点，请求出
的取值范围．
已知在△
中，∠
=30°，
，
,求△的周长. （结果保留根号）
如图，已知△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，求线段DF的长.
已知函数y ="(2m+1)" x+ m-3
(1) 若函数图象经过原点,求m的值
(2) 若函数图象在y轴的交点的纵坐标为－2，求m的值
（3）若函数的图象平行直线y=3x–3，求m的值
（4）若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
暑假的一天，小刚到离家1.2千米的万州体育馆看球赛，进场时，发现门票还放在家中，此时离比赛还有24分钟，于是他立即步行(匀速)回家取票，在家取票用时5分钟，取到票后，他马上骑自行车(匀速)赶往体育馆．已知小刚骑自行车从家赶往体育馆比从体育馆步行回家所用时间少10分钟，骑自行车的速度是步行速度的3倍．
(1)小刚步行的速度(单位：米/分钟)是多少？
(2)小刚能否在球赛开始前赶到体育馆？请通过计算说明理由．
某市采用价格调控的手段达到节约用水的目的，制定如下用水收费标准：每户每月用水不超过6m3，水费按a元/m3收费；若超过6m3,6m3以内的仍按a元/m3收费，超过6m3的部分以b元/m3收费．某户居民5、6月份用水量和水费如下表：
| 月份 |
用水量(m3) |
水费(元) |
| 5 |
5 |
7.5 |
| 6 |
9 |
27 |
设该用户每月用水量为xm3，应交水费y元．
(1)求出a，b的值；
(2)写出用水量不超过6m3和超过6m3时，y与x之间的函数关系式；
(3)若该用户7月份用水量为8m3，他应交多少元水费？