九(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.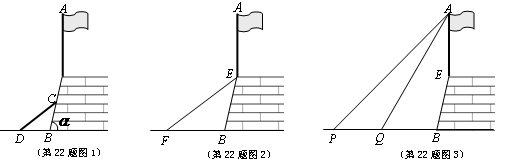
(1)如图1,第一小组用一根木条CD斜靠在护墙上, 使得DB与CB的长度相等, 如果测量得到∠CDB=38°, 求护墙与地面的倾斜角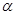 的度数.
的度数.
(2)如图2,第二小组用皮尺量得EF为16米(E为护墙上的端点),EF的中点离地面FB的高度为1.9米, 请你求出E点离地面FB的高度.
(3)如图3,第三小组利用第一、二小组的结果,来测量护墙上旗杆的高度.在点P测得旗杆顶端A的仰角为45°,向前走4米到达Q点,测得A的仰角为60°,求旗杆AE的高度(精确到0.1米).
某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门也大小相同,安全检查时,对4道门进行测试,当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生,当同时开启一道正门和一道侧门时,4分钟内可通过800名学生.求平均每分钟一道正门和一道侧门各可以通过多少名学生?
检查中发现,紧急情况时学生拥挤,出门的效率将降低20%,安全检查规定,在紧急情况下,全大楼学生应在5分钟内同时通过这4道门安全撤离,假设这栋教学楼每间教室最多有45名学生.问:建造的4道门是否符合安全规定?请说明理由.
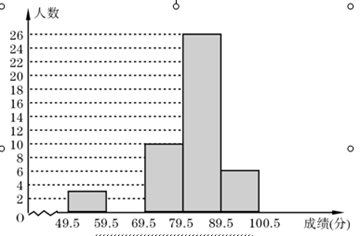
吴老师为了解本班学生的数学学习情况,对某次数学考试成绩(成绩取整数,满分为100分)作了统计,绘制成如下频数分布表和频数分布直方图.
请你根据图表提供的信息,解答下列问题:
| 分组 |
49.5~59.5 |
59.5~69.5 |
69.5~79.5 |
79.5~89.5 |
89.5~100.5 |
合计 |
| 频数 |
3 |
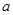 |
10 |
26 |
6 |
 |
| 频率 |
0.06 |
0.10 |
0.20 |
0.52 |
 |
1.00 |
直接写出频数分布表中
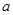 、
、 、
、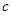 的值;并补全频数分布直方图;
的值;并补全频数分布直方图;如果用扇形统计图表示这次数学考试成绩,那么成绩在69.5~79.5范围内的扇形圆心角的度数为多少度?
放风筝是大家喜爱的一种运动.星期天的上午,小明在大洲广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树CD的树梢上,风筝固定在了D处.此时风筝线AD与水平线的夹角为30°.为了便于观察,小明迅速向前边移动边收线到达了离A处7米的B处,此时风筝线BD与水平线的夹角为45°.已知点A、B、C在同一条直线上,∠ACD=90°.请你求出小明此时所收回的风筝线的长度是多少米?(本题中风筝线均视为线段,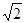 ≈1.4,
≈1.4,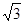 ≈1.7最后结果精确到1米)
≈1.7最后结果精确到1米)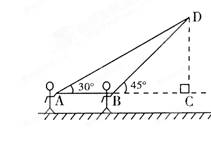
先化简,再求值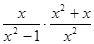 ,其中
,其中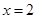 。
。
解不等式组并把解集在数轴上表示出来。