（本小题满分14分）已知直线l：
与双曲线C：
（
）相交于B、D两点，且BD的中点为M（1，3）．
（1）求双曲线C的离心率；
（2）设双曲线C的右顶点为A，右焦点为F，
，试判断△ABD是否为直角三角形，并说明理由．
已知函数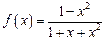
.
（1）若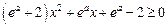
对
恒成立，求
的取值范围；
（2）求证：对于正数、
、
，恒有
.
已知
（1）若
为非零常数，解不等式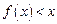
；
（2）当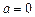
时，不等式
在
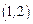上有解，求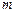
的取值范围.
如图，在四棱椎
中，底面
是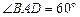
且边长为2的菱形，
侧面
为正三角形，其所在平面垂直于底面.
（1）若G为
边的中点，求证：
平面；
（2）求二面角
的大小；
（3）若E为
的中点，能否在棱
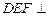上找一点F，使得平面
平面，并证明你的结论.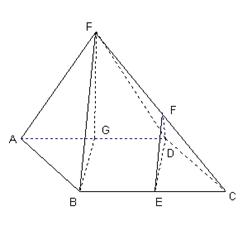
一个人随机将编号为1，2，3，4的四个小球放入编号为1，2，3，4的四个盒子中去，每个盒子放入一球，当盒子编
号与球的编号相同时
叫做放对了，否则叫放错了，设放对了的小球数有
个.
（1）求的分布列；
（2）求的期望与方差.
在
中，
、
、
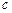分别是角
、
、
的对边，且
.
（1）求角的大小；
（2）若的面积是
，且
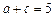，求.