已知在四棱锥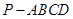 中,底面
中,底面 是矩形,且
是矩形,且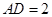 ,
,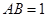 ,
,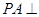 平面
平面 ,
,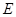 、
、 分别是线段
分别是线段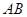 、
、 的中点.
的中点.
(1)证明:
(2)若 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值
的余弦值

已知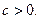 设P:函数
设P:函数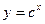 在R上单调递减; Q:不等式
在R上单调递减; Q:不等式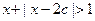 的解集为R,若“P或Q”是真命题,“P且Q”是假命题,求
的解集为R,若“P或Q”是真命题,“P且Q”是假命题,求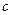 的取值范围.
的取值范围.
[解题思路]:“P或Q”是真命题,“P且Q”是假命题,根据真假表知,P,Q之中一真一假,因此有两种情况,要分类讨论.
分别指出下列复合命题的形式及构成它的简单命题:
(1)3是质数或合数.
(2)他是运动员兼教练员.
(3)相似三角形不一定是全等三角形.
写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并指出所构成的这些复合命题的真假。
(1)p:5是17的约数,q:5是15的约数.
(2)p:方程x2-1=0的解是x="1," q:方程x2-1=0的解是x=-1,
(3)p:不等式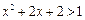 的解集为R,q:不等式
的解集为R,q:不等式 的解集为
的解集为
分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题:
(1)p: 是无理数,q:
是无理数,q:  大于是2
大于是2
(2)p: ,q:
,q:
(3)p:  , q:
, q: 
分别写出下列各组命题构成的“p或q”“p且q”“非p”形式的复合命题:
(1)p:连续的三个整数的乘积能被2整除, q:连续的三个整数的乘积能被3整除.
(2)p:对角线互相垂直的四边形是菱形, q:对角线互相平分的四边形是菱形.