(本小题满分13分)已知椭圆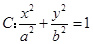
 的离心率为
的离心率为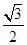 ,直线
,直线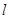 经过椭圆的上顶点
经过椭圆的上顶点 和右顶点
和右顶点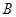 ,并且和圆
,并且和圆 相切.
相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线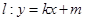 (
( )与椭圆
)与椭圆 相交于
相交于 、
、 两点,以线段
两点,以线段 、
、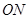 为邻边作平行四边形
为邻边作平行四边形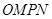 ,其中顶点
,其中顶点 在椭圆
在椭圆 上,(其中
上,(其中 为坐标原点),求
为坐标原点),求 的取值范围.
的取值范围.
(本小题满分12分)如图甲,在平面四边形ABCD中,已知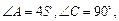
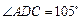 ,
, ,现将四边形ABCD沿BD折起,使
,现将四边形ABCD沿BD折起,使 平面ABD
平面ABD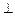
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(Ⅰ)求证:DC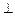 平面ABC;
平面ABC;
(Ⅱ)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
(本小题满分12分)已知 ,其中
,其中 .
.
若 满足
满足 ,且
,且 的图象关于直线
的图象关于直线 对称.
对称.
(Ⅰ)求 的值;
的值;
(Ⅱ)若关于 的方程
的方程 在区间
在区间 上总有实数解,求实数
上总有实数解,求实数 的取值范围.
的取值范围.
(本小题满分12分)
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(Ⅰ)求出表中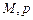 及图中
及图中 的值;
的值;
(Ⅱ)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间 内的人数;
内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间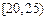 内的概率.
内的概率.
(本小题满分12分).已知圆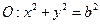 与直线
与直线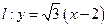 相切。
相切。
(1)求以圆O与y轴的交点为顶点,直线在x轴上的截距为半长轴长的椭圆C方程;
(2)已知点A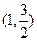 ,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线
,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线
AF的斜率互为相反数;问直线的斜率是否为定值?若是求出这个定值;若不是,请说明理由.
(满分12分)设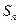 为数列
为数列 的前
的前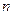 项和,对任意的
项和,对任意的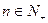 ,都有
,都有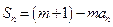
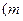 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比
的公比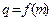 ,数列
,数列 满足
满足 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前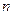 项和
项和 .
.