（本小题满分12分）.已知圆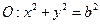
与直线
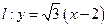相切。
（1）求以圆O与y轴的交点为顶点，直线在x轴上的截距为半长轴长的椭圆C方程;
（2）已知点A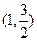
，若直线与椭圆C有两个不同的交点E,F，且直线AE的斜率与直线
AF的斜率互为相反数;问直线的斜率是否为定值？若是求出这个定值;若不是，请说明理由.
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸缩变换.
(1)求矩阵M的特征值及相应的特征向量.
(2)求逆矩阵M-1以及椭圆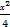
+
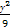=1在M-1的作用下的新曲线的方程.
已知矩阵M=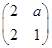
,其中a∈R,若点P(1,-2)在矩阵M的变换下得到点P'(-4,0),
(1)求实数a的值.
(2)求矩阵M的特征值及其对应的特征向量.
求矩阵M=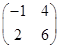
的特征值和特征向量.
已知2×2矩阵A有特征值λ1=3及其对应的一个特征向量α1=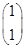
,特征值λ2=-1及其对应的一个特征向量α2=
,求矩阵A的逆矩阵A-1.
已知△ABC,A(-1,0),B(3,0),C(2,1),对它先作关于x轴的反射变换,再将所得图形绕原点逆时针旋转90°.
(1)分别求两次变换所对应的矩阵M1,M2.
(2)求△ABC在两次连续的变换作用下所得到的△A'B'C'的面积.