(本小题满分12分)设为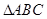 的内角
的内角 、
、 、
、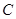 所对的边分别为
所对的边分别为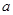 、
、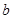 、
、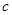 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求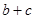 的最值.
的最值.
(本小题满分13分)已知函数 .
.
(1)若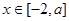 ,求
,求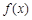 的值域;
的值域;
(2)若存在实数t,当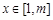 ,
,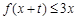 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分13分)某校高一年级开设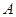 ,
,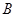 ,
,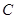 ,
,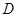 ,
,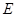 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选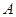 课程,不选
课程,不选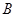 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中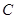 课程且乙同学未选中
课程且乙同学未选中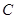 课程的概率;
课程的概率;
(Ⅱ)用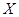 表示甲、乙、丙选中
表示甲、乙、丙选中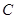 课程的人数之和,求
课程的人数之和,求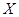 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)万州区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: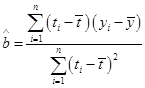 ,
,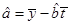
(本小题满分10分)已知复数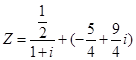
(1)求复数Z的模;
(2)若复数Z是方程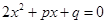 的一个根,求实数
的一个根,求实数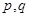 的值?
的值?
(本小题满分13分)已知函数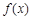 满足
满足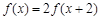 ,且当
,且当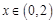 时,
时,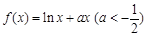 ,当
,当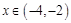 时,
时,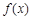 的最大值为
的最大值为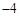 .
.
(1)求实数a的值;
(2)设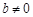 ,函数
,函数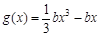 ,
,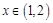 .若对任意
.若对任意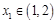 ,总存在
,总存在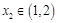 ,使
,使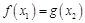 ,求实数b的取值范围.
,求实数b的取值范围.