(本小题满分12分)已知等差数列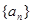 的公差不为零,
的公差不为零, ,等比数列
,等比数列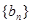 的前3项满足
的前3项满足 .
.
(Ⅰ)求数列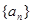 与
与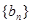 的通项公式;
的通项公式;
(Ⅱ)设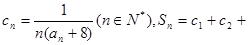
 ,求Sn.
,求Sn.

(本小题满分14分)
在平面直角坐标系 中,已知圆
中,已知圆 和圆
和圆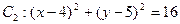 .
.
(1)若直线 过点
过点 ,且被圆
,且被圆
 截得的弦长为
截得的弦长为 ,求直线
,求直线 的方程;
的方程;
(2)在平面内是否存在一点 ,使得过点
,使得过点 有无穷多对互相垂直的直线
有无穷多对互相垂直的直线 和
和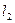 ,它们分别与圆
,它们分别与圆 和圆
和圆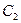 相交,且直线
相交,且直线 被圆
被圆 截得的弦长的
截得的弦长的 倍与直线
倍与直线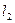 被圆
被圆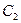 截得的弦长相等?若存在,求出所有满足条件的
截得的弦长相等?若存在,求出所有满足条件的 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
 |
(本小题满分14分)
如图,已知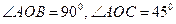 ,
,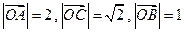 .
.
(1)试用向量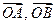 来表示向量
来表示向量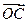 ;
;
(2)若向量 ,
,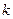
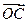 的终点在一条直线上,
的终点在一条直线上,
求实数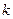 的值;
的值;
(3 )设
)设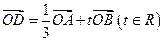 ,当
,当 、
、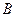 、
、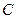 、
、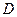 四点共圆时, 求
四点共圆时, 求 的值.
的值.
 |
( 本小题满分13分)
本小题满分13分)
从某校高一年级参加期末考试的学生中抽出 名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(1)根据频率分布直方图估计这次考试该年级的数学平均分;
(2) 已知在[90,100]内的学生的数学成绩都不相同,且都在95分以上(不含95分),现用简单随机抽样方法,从 这
这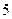 个数中任取
个数中任取 个数,求这
个数,求这 个数恰好是两名学生的数学成绩的概率.
个数恰好是两名学生的数学成绩的概率.
 |
(本小题满分13分)
已知向量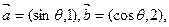 满足
满足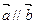 ,其中
,其中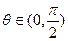 .
.
(1)求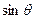 和
和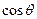 的值;
的值;
(2)若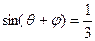 ,求
,求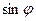 的值.
的值.