(本小题满分12分) 已知单调递增的等比数列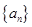 满足:
满足: ,且
,且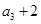 是
是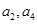 的等差中项.
的等差中项.
(Ⅰ)求数列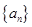 的通项公式;
的通项公式;
(Ⅱ)若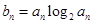 ,
,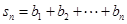 ,求
,求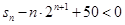 成立的正整数
成立的正整数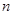 的最小值.
的最小值.
(14分)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率 .直线
.直线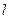 :
: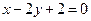 与椭圆C相交于
与椭圆C相交于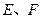 两点, 且
两点, 且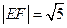
(1)求椭圆C的方程
(2)点P(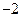 ,0),A、B为椭圆C上的动点,当
,0),A、B为椭圆C上的动点,当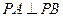 时,求证:直线AB恒过一个定点.并求出该定点的坐标.
时,求证:直线AB恒过一个定点.并求出该定点的坐标.
(13分)已知函数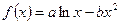 图象上一点P(2,
图象上一点P(2, )处的切线方程为
)处的切线方程为
(1)求 的值(2)若方程
的值(2)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求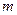 的取值范围(其中
的取值范围(其中 为自然对数的底)
为自然对数的底)
(12分)如图,在棱长为2的正方体ABCD -A1B1C1D1中,E、F分别为A1D1和CC1 的中点.
(1)求证:EF∥平面ACD1
(2)求三棱锥E-ACD1的体积与正方体ABCD -A1B1C1D1的体积之比
(12分)某电视台综艺频道主办一种有奖过关游戏,该游戏设有两关,只有过了第一关,才能玩第二关,每关最多玩两次,连续两次失败者被淘汰出局.过关者可获奖金,只过第一关获奖金900元,两关全过获奖金3600元.某同学有幸参与了上述游戏,且该同学每一次过关的概率均为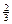 ,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
,各次过关与否互不影响.在游戏过程中,该同学不放弃所有机会.
(1)求该同学仅获得900元奖金的概率
(2)若该同学已顺利通过第一关,求他获得3600元奖金的概率
已知向量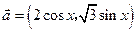 ,
,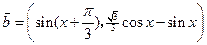 ,函数
,函数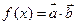
(1)求函数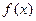 的最小正周期
的最小正周期
|
(2)若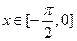 时,求
时,求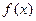 的单调递减区间
的单调递减区间