(本小题满分14分)已知函数 (
( 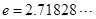 是自然对数的底数),
是自然对数的底数), .
.
(1)若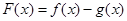 ,求
,求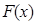 的极值;
的极值;
(2)对任意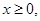 证明:
证明: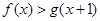 ;
;
(3)对任意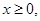 都有
都有 成立,求实数
成立,求实数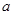 的取值范围.
的取值范围.
平行四边形 中,
中, 且
且 以
以 为折线,把
为折线,把 折起,使平面
折起,使平面 平面
平面 ,连接
,连接

(1)求证: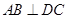 ;
;
(2)求二面角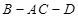 的余弦值.
的余弦值.
已知函数 的图像在点
的图像在点 处的切线斜率为10.
处的切线斜率为10.
(1)求实数 的值;
的值;
(2)判断方程 根的个数,并证明你的结论;
根的个数,并证明你的结论;
(21)探究: 是否存在这样的点 ,使得曲线
,使得曲线 在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右两部分分别位于曲线在该点处切线的两侧? 若存在,求出点A的坐标;若不存在,说明理由.
已知椭圆C的中心在原点,焦点在 轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
(1)求椭圆C的方程;
(2)已知点P的坐标为P(-4,0), 过P点的直线L与椭圆C相交于M、N两点,当线段MN的中点G落在正方形内(包含边界)时,求直线L的斜率的取值范围.
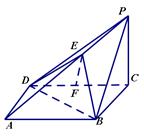
如图四棱锥 中,底面
中,底面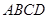 是平行四边形,
是平行四边形,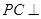 平面
平面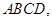
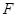 是
是 的中点,
的中点,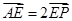 .
.
(1)试判断直线 与平面
与平面 的位置关系,并予以证明;
的位置关系,并予以证明;
(2)若四棱锥 体积为
体积为
 ,
, ,求证:平面
,求证:平面 .
.
甲、乙两人玩一种游戏:在装有质地、大小完全相同,编号分别为1,2,3,4,5五个球的口袋中,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号和为6的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.