甲、乙、丙、丁四位好友约好出去游玩,为了增加乐趣,游玩的费用四人约好:每人掷一枚质地均匀的骰子决定出资的数值,掷出的点数为1或2的人出资200元,掷出的点数大于2的人出资100元;
(1)求这4个人中恰好有两人出资200元的概率;
(2)用 分别表示四个人出资200元、100元的人数,记
分别表示四个人出资200元、100元的人数,记 ,求
,求 的概率分布列和数学期望;
的概率分布列和数学期望;
已知数列 的首项
的首项 ,
, ,
, .
.
(1)求 的通项公式;
的通项公式;
(2)证明:对任意的 ,
, ,
, ;
;
(3)证明: .
.
如图,设抛物线方程为 直线
直线 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。
(1)求证:A,M,B三点的横坐标成等差数列;
(2)已知当M点的坐标为 时,
时, ,求此时抛物线的方程;
,求此时抛物线的方程;
(3)是否存在点M,使得点C关于直线AB的对称点D在抛物线 上,其中,点C满足
上,其中,点C满足 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
已知函数 。(1)求函数
。(1)求函数 的单调区间和值域;
的单调区间和值域;
(2)设 ,函数
,函数 ,若对于任意
,若对于任意 总存在
总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围。
的取值范围。
如图,等边 与直角梯形ABDE所在平面垂直,
与直角梯形ABDE所在平面垂直, ,AE⊥AB,
,AE⊥AB, ,O为AB的中点.
,O为AB的中点.
|

 ;
;
 的余弦值.
的余弦值.
在一次抗洪抢险中准备用射击的方法引爆从上游漂流而下的一个巨大汽油罐。已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆。每次射击是相互独立的,且命中的概率都是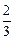 。
。
(1)求油罐被引爆的概率;
(2)如果引爆或子弹打光停止射击,设射击次数为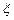 ,求
,求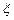 的分布列及数学期望。
的分布列及数学期望。