(本小题满分12分)一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1,2,3,4,5,现从盒子中随机抽取卡片.
(1)从盒中依次抽取两次卡片,每次抽取一张,取出的卡片不放回,求两次取到的卡片的数字既不全是奇数,也不全是偶数的概率;
(2)若从盒子中有放回的抽取3次卡片,每次抽取一张,求恰有两次取到卡片的数字为偶数的概率;
(3)从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当取到记有奇数的卡片即停止抽取,否则继续抽取卡片,求抽取次数 的分布列和期望.
的分布列和期望.
某个海边旅游景点,有小型游艇出租供游客出海游玩,收费标准如下:租用时间不超过2小时收费100,超过2小时的部分按每小时100收取(不足一小时按一小时计算).现甲、乙两人独立来该景点租用小型游艇,各租一次.设甲、乙租用不超过两小时的概率分别为 ,
, ;租用2小时以上且不超过3小时的概率分别为
;租用2小时以上且不超过3小时的概率分别为 ,
, ,且两人租用的时间都不超过4小时.
,且两人租用的时间都不超过4小时.
(Ⅰ)求甲、乙两人所付费用相同的概率;
(Ⅱ)设甲、乙两人所付的费用之和为随机变量 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
已知 分别在射线
分别在射线 (不含端点
(不含端点 )上运动,
)上运动,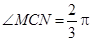 ,在
,在 中,角
中,角 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 .
.
(Ⅰ)若 、
、 、
、 依次成等差数列,且公差为2.求
依次成等差数列,且公差为2.求 的值;
的值;
(Ⅱ)若 ,
, ,试用
,试用 表示
表示 的周长,并求周长的最大值.
的周长,并求周长的最大值.
(本小题满分13分)已知函数 ,其中
,其中 .
.
(1)当 时,求函数
时,求函数 的图象在点
的图象在点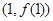 处的切线方程;
处的切线方程;
(2)当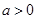 时,证明:存在实数
时,证明:存在实数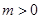 ,使得对于任意的实数
,使得对于任意的实数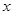 ,都有
,都有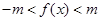 成立;
成立;
(3)当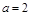 时,是否存在实数
时,是否存在实数 ,使得关于
,使得关于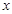 的方程
的方程 仅有负实数解?当
仅有负实数解?当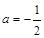 时的情形又如何?(只需写出结论).
时的情形又如何?(只需写出结论).
(本小题满分14 分)设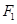 ,
, 分别为椭圆
分别为椭圆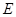 :
: 的左、右焦点,点
的左、右焦点,点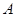 为椭圆
为椭圆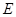 的左顶点,点
的左顶点,点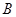 为椭圆
为椭圆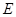 的上顶点,且
的上顶点,且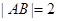 .
.
(1)若椭圆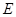 的离心率为
的离心率为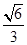 ,求椭圆
,求椭圆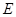 的方程;
的方程;
(2)设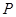 为椭圆
为椭圆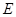 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线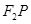 与
与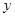 轴相交于点
轴相交于点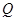 ,若以
,若以 为直径的圆经过点
为直径的圆经过点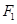 ,证明:点
,证明:点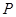 在直线
在直线 上.
上.
(本小题满分13 分)某厂商调查甲、乙两种不同型号电视机在10 个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.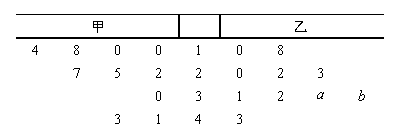
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)求在这10个卖场中,甲型号电视机的“星级卖场”的个数;
(2)若在这10个卖场中,乙型号电视机销售量的平均数为26.7,求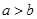 的概率;
的概率;
(3)若 ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为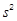 ,根据茎叶图推断
,根据茎叶图推断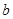 为何值时,
为何值时,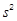 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
(注:方差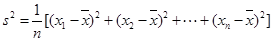 ,其中
,其中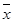 为
为 ,
,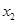 ,…,
,…,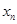 的平均数)
的平均数)