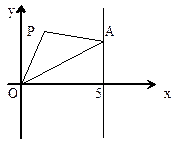已知 分别在射线
分别在射线 (不含端点
(不含端点 )上运动,
)上运动,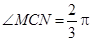 ,在
,在 中,角
中,角 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 .
.
(Ⅰ)若 、
、 、
、 依次成等差数列,且公差为2.求
依次成等差数列,且公差为2.求 的值;
的值;
(Ⅱ)若 ,
, ,试用
,试用 表示
表示 的周长,并求周长的最大值.
的周长,并求周长的最大值.
已知全集 ,集合
,集合 ,
, .
.
(1)若 ,求实数
,求实数 的值;
的值;
(2)若“ ”是“
”是“ ”的必要不充分条件,求实数
”的必要不充分条件,求实数 的取值范围.
的取值范围.
某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段 ,
, …
… 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
(1)求出物理成绩低于50分的学生人数
(2)估计这次考试物理学科及格率(60分及以上为及格)
(3)从物理成绩不及格的学生中选1人,求他们成绩至少有一个低于50分的概率
 |
(本小题满分16分)
(1)用二项式定理证明: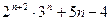
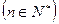 能被25整除
能被25整除
(2) (
(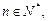 且
且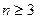
(本小题满分16分)
随机抽取某厂的某种产品400件,经质检,其中有一等品252件、二等品100件、三等品40件、次品8件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为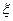
(1)求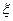 的分布列和数学期望
的分布列和数学期望
(2)经技术革新后,仍有四个等级的产品,但次品率降为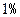 ,一等品率提高为
,一等品率提高为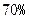 .如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
(本小题满分16分)
如图,点A在直线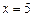 上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按顺时针方向排列),求点P的轨迹方程
上移动,等腰△OPA的顶角∠OPA为120°(O,P,A按顺时针方向排列),求点P的轨迹方程