已知抛物线
（1）若点
是抛物线
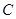上一点，求证过点
的抛物线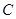的切线方程为：
；
（2）点
是抛物线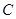准线上一点，过点作抛物线的两条切线，切点分别为
，求
的最小值，并求相应的点的坐标．
（本小题满分12分）
如图，在四棱锥P-ABCD中，底面ABCD为正方形，且PD
平面ABCD，PD=AB=1，E，F分别是PB，AD的中点
（I）证明:EF//平面PCD
（II）求二面角B-CE-F的大小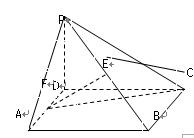
（文）已知甲，乙两名射击运动员各自独立地射击1次命中10环的概率分别为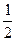
，
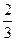
（I）求乙在第3次射击时（每次射击相互独立）才首次命中10环的概率
（II）若甲乙两名运动员各自独立地射击1次，求两人中恰有一人命中10环的概率
（本小题满分12分）
（理）已知甲，乙两名射击运动员各自独立地射击1次，命中10环的概率分别为
，x（x＞）；且乙运动员在2次独立射击中恰有1次命中10环的概率为
（I）求x的值
（II）若甲，乙两名运动员各自独立地射击1次，设两人命中10环的次数之和为随机变量ξ，求ξ的分布列及数学期望
（本小题满分12分）在△ABC中,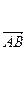
·
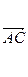=1，
·
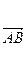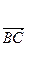=-3
（I）求△ABC的边AB的长
（II）求
的值
已知函数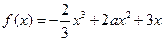
.
(Ⅰ)当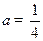
时，求函数
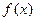在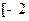
，
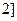上的最大值、最小值；
(Ⅱ)令
，若
在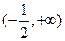
上单调递增，求实数
的取值范围.