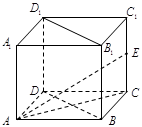设椭圆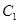 :
: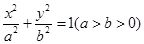 的左、右焦点分别是
的左、右焦点分别是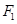 、
、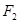 ,下顶点为
,下顶点为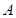 ,线段
,线段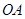 的中点为
的中点为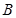 (
(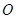 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线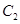 :
: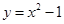 与
与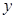 轴的交点为
轴的交点为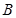 ,且经过
,且经过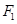 、
、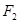 两点.
两点.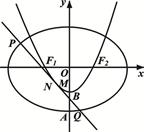
(Ⅰ)求椭圆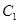 的方程;
的方程;
(Ⅱ)设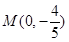 ,
,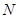 为抛物线
为抛物线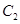 上的一动点,过点
上的一动点,过点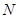 作抛物线
作抛物线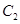 的切线交椭圆
的切线交椭圆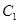 于
于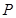 、
、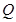 两点,求
两点,求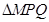 面积的最大值.
面积的最大值.
已知函数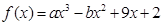 ,若
,若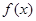 在
在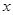 =1处的切线方程为
=1处的切线方程为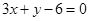 。
。
(1) 求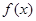 的解析式及单调区间;
的解析式及单调区间;
(2) 若对任意的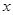

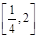 都有
都有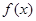 ≥
≥ 成立,求函数
成立,求函数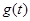 =
=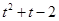 的最值。
的最值。
设 、
、 是椭圆
是椭圆 上的两点,点
上的两点,点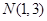 是线段
是线段 的中点,线段
的中点,线段 的垂直平分线与椭圆相交于
的垂直平分线与椭圆相交于 、
、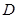 两点.
两点.
(Ⅰ)求直线 的方程;
的方程;
(Ⅱ)求以线段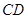 的中点
的中点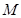 为圆心且与直线
为圆心且与直线 相切的圆的方程.
相切的圆的方程.
已知等差数列{an}的前三项为 ,记前n项和为Sn
,记前n项和为Sn
(Ⅰ)设 ,求a和k的值;
,求a和k的值;
(Ⅱ)设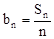 ,求
,求 的值
的值
甲、乙两人各抛掷一次正方体骰子(它们的六个面分别标有数字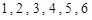 ),设甲、乙所抛掷骰子朝上的面的点数分别为
),设甲、乙所抛掷骰子朝上的面的点数分别为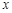 、
、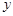 ,那么。
,那么。
(I)共有多少种不同的结果?。
(II)请列出满足复数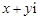 的实部大于虚部的所有结果。。
的实部大于虚部的所有结果。。
(III)满足复数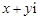 的实部大于虚部的概率是多少?
的实部大于虚部的概率是多少?
正方体 ,
, ,
, 为棱
为棱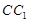 的中点,AC与BD交于点O.(1)求证:
的中点,AC与BD交于点O.(1)求证:
(2)求证: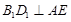 ;
;
(3)求三棱锥 的体积.
的体积.