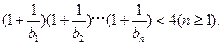(本小题满分7分)选修4—5:不等式选讲
已知函数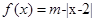 ,
,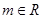 ,且
,且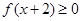 的解集为
的解集为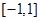 .
.
(Ⅰ)求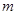 的值;
的值;
(Ⅱ)若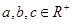 ,且
,且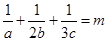 ,求
,求 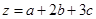 的最小值.
的最小值.
(本小题满分12分)
已知函数
(Ⅰ)若函数 在
在 是增函数,导函数
是增函数,导函数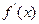 在
在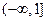 上是减函数,求
上是减函数,求 的值;
的值;
(Ⅱ)令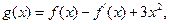 求
求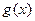 的单调区间.
的单调区间.
(本小题满分13分 )
已知四棱锥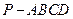 的底面是边长为2的正方形,
的底面是边长为2的正方形,
面
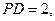
 分别为
分别为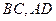 的中点,
的中点,
(Ⅰ)求直线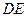 与面
与面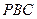 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求二面角 的正切值.
的正切值.
(本小题满分13分)
在一次数学考试中,共有10道选择题,每题均有四个选项,其中有且只有一个选项是正确的,评分标准规定:“每道题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有6道题是正确的,其余题目中:有两道题可判断两个选项是错误的,有一道可判断一个选项是错误的,还有一道因不理解题意只好乱猜,请求出该考生:
(Ⅰ)得50分的概率;
(Ⅱ)得40分的概率.
(本小题满分13分)
已知 为
为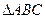 的三内角,且其对边分别为
的三内角,且其对边分别为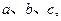 若
若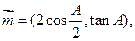
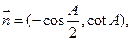 且
且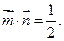
(Ⅰ)求角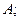
(Ⅱ)若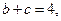
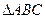 的面积为
的面积为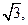 求
求
(本小题满分12分)
设各项为正的数列 满足:
满足: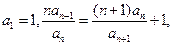 令
令

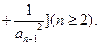
(Ⅰ)求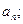
(Ⅱ)求证: