(本小题满分14分)已知椭圆的中心在坐标原点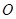 ,长轴长为
,长轴长为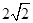 ,离心率
,离心率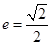 ,过右焦点
,过右焦点 的直线
的直线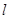 交椭圆于
交椭圆于 ,
,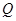 两点.
两点.
(1)求椭圆的方程;
(2)当直线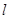 的斜率为1时,求
的斜率为1时,求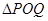 的面积;
的面积;
(3)若以 ,
, 为邻边的平行四边形是矩形,求满足该条件的直线
为邻边的平行四边形是矩形,求满足该条件的直线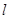 的方程.
的方程.
(本小题满分12分) 的内角
的内角 所对的边分别为
所对的边分别为 ,向量
,向量 与
与 平行.
平行.
(Ⅰ)求 ;
;
(Ⅱ)若 求
求 的面积.
的面积.
(本小题满分12分)某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
(Ⅰ)请在答题卡上将上表数据补充完整,并直接写出函数 的解析式;
的解析式;
(Ⅱ)将 图象上所有点向左平行移动
图象上所有点向左平行移动 个单位长度,得到
个单位长度,得到 图象,求
图象,求 的图象离原点
的图象离原点 最近的对称中心.
最近的对称中心.
(本小题满分10分)已知函数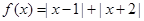
(Ⅰ)解关于 的不等式
的不等式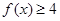 ;
;
(Ⅱ)若关于 的不等式
的不等式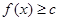 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数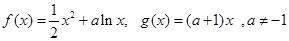 .
.
(1)若函数 在区间
在区间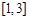 上都是单调函数且它们的单调性相同,求实数
上都是单调函数且它们的单调性相同,求实数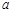 的取值范围;
的取值范围;
(2)若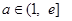 ,设
,设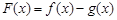 ,求证:当
,求证:当 时,不等式
时,不等式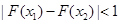 成立.
成立.
(本小题满分12分)已知函数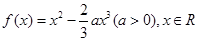
(1)求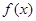 的单调区间和极值;
的单调区间和极值;
(2)若对于任意的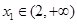 ,都存在
,都存在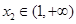 ,使得
,使得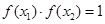 ,求
,求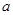 的取值范围.
的取值范围.