已知函数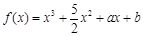 (
( 为常数),其图象是曲线
为常数),其图象是曲线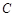 .
.
(1)当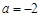 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(2)设函数 的导函数为
的导函数为 ,若存在唯一的实数
,若存在唯一的实数 ,使得
,使得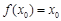 与
与 同时成立,求实数
同时成立,求实数 的取值范围;
的取值范围;
(3)已知点 为曲线
为曲线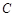 上的动点,在点
上的动点,在点 处作曲线
处作曲线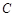 的切线
的切线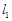 与曲线
与曲线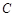 交于另一点
交于另一点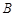 ,在点
,在点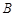 处作曲线
处作曲线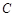 的切线
的切线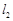 ,设切线
,设切线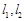 的斜率分别为
的斜率分别为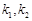 .问:是否存在常数
.问:是否存在常数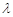 ,使得
,使得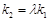 ?若存在,求出
?若存在,求出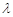 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
在“2013魅力新邢台”青少年才艺表演评比活动中,参赛选手成绩的茎叶图和频率分布直方图,都受到不同程度的损坏,回答问题

(1)求参赛总人数和频率分布直方图中 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图;
(2)若要从分数在 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在 之间的概率.
之间的概率.
(已知椭圆
 经过点
经过点 其离心率为
其离心率为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆 相交于A、B两点,以线段
相交于A、B两点,以线段 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 上,
上, 为坐标原点.求
为坐标原点.求 到直线
到直线 距离的最小值.
距离的最小值.
在一次商贸交易会上,商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖.
(1)若抽奖规则是从一个装有2个红球和4个白球的袋中无放回地取出2个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在9:00~9:40之间赶到,乙计划在9:20~10:00之间赶到,求甲比乙提前到达的概率.
已知双曲线的方程是 ,
,
(1)求此双曲线的焦点坐标、离心率和渐近线方程;
(2)点 在双曲线上,满足
在双曲线上,满足 ,求
,求 的大小.
的大小.
已知椭圆 经过点
经过点 ,
,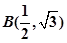 .
.
(Ⅰ)求椭圆 的方程;(Ⅱ)设
的方程;(Ⅱ)设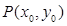 为椭圆
为椭圆 上的动点,求
上的动点,求 的最大值.
的最大值.